Learning Scientific Programming with Python (2nd edition)
E8.3: Drum vibrations with Bessel functions
The vibrations of a thin circular membrane stretched across a rigid circular frame (such as a drum head) can be described as normal modes written in terms of Bessel functions: $$ z(r, \theta; t) = A J_n(kr) \sin n\theta \cos k\nu t, $$ where $(r, \theta)$ describes a position in polar co-ordinates with the origin at the centre of the membrane, $t$ is time and $v$ is a constant depending on the tension and surface density of the drum. The modes are labelled by integers $n = 0, 1, \cdots$ and $m = 1, 2, 3, \cdots$ where $k$ is the $m$th zero of $J_n$.
The following program produces a plot of the displacement of the membrane in the $n=3, m=2$ normal mode at time $t=0$.
import numpy as np
from scipy.special import jn, jn_zeros
import matplotlib.pyplot as plt
# Allow calculations up to m = mmax
mmax = 5
def displacement(n, m, r, theta):
"""
Calculate the displacement of the drum membrane at (r, theta; t=0)
in the normal mode described by integers n >= 0, 0 < m <= mmax.
"""
# Pick off the mth zero of Bessel function Jn
k = jn_zeros(n, mmax + 1)[m]
return np.sin(n * theta) * jn(n, r * k)
# Positions on the drum surface are specified in polar co-ordinates
r = np.linspace(0, 1, 100)
theta = np.linspace(0, 2 * np.pi, 100)
# Create arrays of cartesian co-ordinates (x, y) ...
x = np.array([rr * np.cos(theta) for rr in r])
y = np.array([rr * np.sin(theta) for rr in r])
# ... and vertical displacement (z) for the required normal mode at
# time, t = 0
n, m = 3, 2
z = np.array([displacement(n, m, rr, theta) for rr in r])
plt.axis("equal")
plt.contour(x, y, z)
plt.show()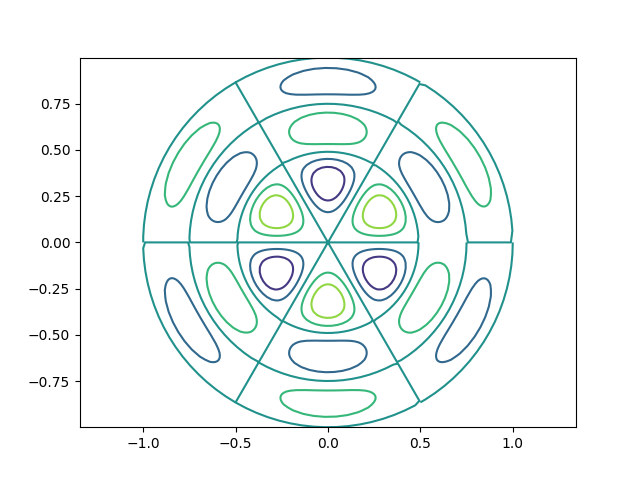
Vibrational normal mode for n=3, m=2 of a circular drum.