Learning Scientific Programming with Python (2nd edition)
E6.11: The height of liquid in a spherical tank
The tanks used in the storage of cryogenic liquids and rocket fuel are often spherical (why?). Suppose a particular spherical tank has a radius $R$ and is filled with a liquid to a height $h$. It is (fairly) easy to find a formula for the volume of liquid from the height:
$$
V = \pi Rh^2 - \frac{1}{3}\pi h^3.
$$
Suppose that there is a constant flow of liquid from the tank at a rate $F = -\mathrm{d}V/\mathrm{d}t$. How does the height of liquid, $h$, vary with time? Differentiating the above equation with respect to $t$ leads to
$$
(2\pi Rh - \pi h^2)\frac{\mathrm{d}h}{\mathrm{d}t} = -F.
$$
If we start with a full tank ($h=2R$) at time $t=0$, this ordinary differential equation may be integrated to yield the equation
$$
-\frac{1}{3}\pi h^3 + \pi R h^2 + \left(Ft - \frac{4}{3}\pi R^3\right) = 0,
$$
a cubic polynomial in $h$. Since this equation cannot be inverted analytically for $h$, let's use NumPy's Polynomial class to find $h(t)$, given a tank of radius $R = 1.5\;\mathrm{m}$ from which liquid is being drawn at $200\;\mathrm{cm^3\,s^{-1}}$.
The total volume of liquid in the full tank is $V_0 = \frac{4}{3}\pi R^3$. Clearly, the tank is empty when $h=0$, which occurs at time $T = V_0/F$, since the flow rate is constant. At any particular time, $t$, we can find $h$ by finding the roots of this equation.
import numpy as np
import matplotlib.pyplot as plt
Polynomial = np.polynomial.Polynomial
# Radius of the spherical tank in m.
R = 1.5
# Flow rate out of the tank, m^3.s-1.
F = 2.0e-4
# Total volume of the tank
V0 = 4 / 3 * np.pi * R**3
# Total time taken for the tank to empty.
T = V0 / F
# coefficients of the quadratic and cubic terms
# of p(h), the polynomial to be solved for h.
c2, c3 = np.pi * R, -np.pi / 3
N = 100
# Array of N time points between 0 and T inclusive.
time = np.linspace(0, T, N)
# Create the corresponding array of heights h(t).
h = np.zeros(N)
# The initial height of the liquid is 2R if the sphere is full.
h[0] = 2 * R
# Solve for subsequent times.
for i, t in enumerate(time[1:], start=1):
c0 = F * t - V0
p = Polynomial([c0, 0, c2, c3])
# Find the three roots to this polynomial.
roots = p.roots()
# We want the one root for which 0 <= h <= 2R.
h[i] = roots[(0 <= roots) & (roots <= 2 * R)][0]
plt.plot(time, h, "o")
plt.xlabel("Time /s")
plt.ylabel("Height in tank /m")
plt.show()For each time point between $t=0$ and $t=T$, we find the roots of the above cubic polynomial. Only one of the roots is physically meaningful, in that $0 \le h \le 2R$ (the height of the level of liquid cannot be negative or greater than the diameter of the tank), so we extract that root (by boolean indexing) store it in the array $h$.
Finally, we plot $h$ as a function of time.
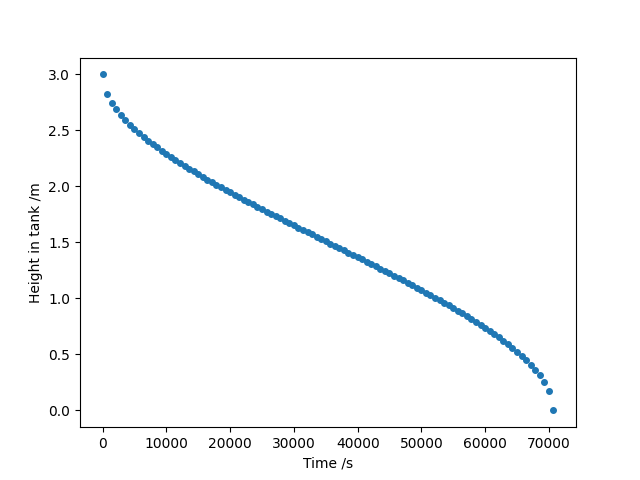
The height of liquid in a spherical tank being drained at a constant rate.