Posted by: christian on 28 Aug 2019
The magnetic field due to a magnetic dipole moment, $\boldsymbol{m}$ at a point $\boldsymbol{r}$ relative to it may be written $$ \boldsymbol{B}(\boldsymbol{r}) = \frac{\mu_0}{4\pi r^3}[3\boldsymbol{\hat{r}(\boldsymbol{\hat{r}} \cdot \boldsymbol{m}) - \boldsymbol{m}}], $$ where $\mu_0$ is the vacuum permeability. In geomagnetism, it is usual to write the radial and angular components of $\boldsymbol{B}$ as: $$ \begin{align*} B_r & = -2B_0\left(\frac{R_\mathrm{E}}{r}\right)^3\cos\theta, \\ B_\theta & = -B_0\left(\frac{R_\mathrm{E}}{r}\right)^3\sin\theta, \\ B_\phi &= 0, \end{align*} $$ where $\theta$ is polar (colatitude) angle (relative to the magnetic North pole), $\phi$ is the azimuthal angle (longitude), and $R_\mathrm{E}$ is the Earth's radius, about 6370 km. See below for a derivation of these formulae.
With this definition, $B_0$ denotes the magnitude of the mean value of the field at the magnetic equator on the Earth's surface, about $31.2\; \mathrm{\mu T}$.
With these definitions, we can plot the dipole component of the Earth's magnetic field as a Matplotlib streamplot. We first construct a meshgrid of $(x,y)$ coordinates and convert them into polar coordinates with the relations:
$$
\begin{align*}
r &= \sqrt{x^2 + y^2},\\
\theta &= \mathrm{atan2}(y/x),
\end{align*}
$$
where the two-argument arctangent function, $\mathrm{atan2}$, is implemented in NumPy as arctan2. We can then use the formulae above to calculate $B_r$ and $B_\theta$ and convert back to Cartesian coordinates to plot the streamplot. The $\theta$ coordinate is offset by $\alpha = 9.6^\circ$ to account for the current tilt of the Earth's magnetic dipole with respect to its rotational axis.
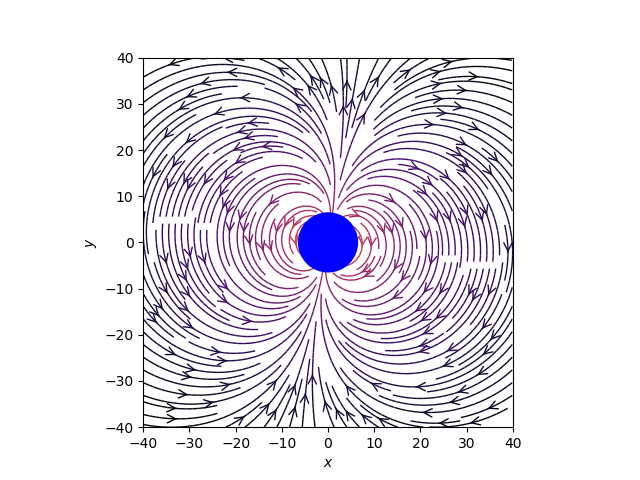
import sys
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
# Mean magnitude of the Earth's magnetic field at the equator in T
B0 = 3.12e-5
# Radius of Earth, Mm (10^6 m: mega-metres!)
RE = 6.370
# Deviation of magnetic pole from axis
alpha = np.radians(9.6)
def B(r, theta):
"""Return the magnetic field vector at (r, theta)."""
fac = B0 * (RE / r)**3
return -2 * fac * np.cos(theta + alpha), -fac * np.sin(theta + alpha)
# Grid of x, y points on a Cartesian grid
nx, ny = 64, 64
XMAX, YMAX = 40, 40
x = np.linspace(-XMAX, XMAX, nx)
y = np.linspace(-YMAX, YMAX, ny)
X, Y = np.meshgrid(x, y)
r, theta = np.hypot(X, Y), np.arctan2(Y, X)
# Magnetic field vector, B = (Ex, Ey), as separate components
Br, Btheta = B(r, theta)
# Transform to Cartesian coordinates: NB make North point up, not to the right.
c, s = np.cos(np.pi/2 + theta), np.sin(np.pi/2 + theta)
Bx = -Btheta * s + Br * c
By = Btheta * c + Br * s
fig, ax = plt.subplots()
# Plot the streamlines with an appropriate colormap and arrow style
color = 2 * np.log(np.hypot(Bx, By))
ax.streamplot(x, y, Bx, By, color=color, linewidth=1, cmap=plt.cm.inferno,
density=2, arrowstyle='->', arrowsize=1.5)
# Add a filled circle for the Earth; make sure it's on top of the streamlines.
ax.add_patch(Circle((0,0), RE, color='b', zorder=100))
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.set_xlim(-XMAX, XMAX)
ax.set_ylim(-YMAX, YMAX)
ax.set_aspect('equal')
plt.show()
Derivation
For now, consider the dipole to lie along the $y$-axis: $\boldsymbol{m} = m\boldsymbol{\hat{\jmath}}$ and define $\boldsymbol{B_0}$ to be the field perpendicular to $\boldsymbol{m}$ at a distance $R_\mathrm{E}$ from it (i.e. on the Earth's magnetic equator): $$ \boldsymbol{B_0} = -\frac{\mu_0m}{4\pi R_\mathrm{E}^3} \boldsymbol{\hat{\jmath}} = B_0\boldsymbol{\hat{\jmath}}. $$ Then, $$ \boldsymbol{B}(\boldsymbol{r}) = -B_0 \left(\frac{R_\mathrm{E}}{r}\right)^3 [3\cos\theta \boldsymbol{\hat{r}} - \boldsymbol{\hat{\jmath}}]. $$ The radial component of the magnetic field is therefore $$ B_r = \boldsymbol{B}\cdot\boldsymbol{\hat{r}} = -B_0\left(\frac{R_\mathrm{E}}{r}\right)^3[3\cos\theta - \cos\theta] = -2B_0\left(\frac{R_\mathrm{E}}{r}\right)^3\cos\theta, $$ Its angular component is perpendicular to this: $$ B_\theta = \boldsymbol{B}\cdot\boldsymbol{\hat{\theta}} = - B_0 \left(\frac{R_\mathrm{E}}{r}\right)^3 [-\boldsymbol{\hat{\jmath}} \cdot \boldsymbol{\hat{\theta}}] = -B_0\left(\frac{R_\mathrm{E}}{r}\right)^3\sin\theta. $$ Finally, $B_\phi = 0$: the field is symmetric about the axis of the dipole.
Further Reading
- Wikipedia article on the dipole model of the Earth's magnetic field
- M. Walt, Introduction to Geomagnetically Trapped Radiation (1994), Cambridge University Press.
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
Zion_Samurai 4 years, 7 months ago
As I see it, as you may allow. I think that the magnetic field of the Earth is reversed, and some of the beginning and tail end are not connected to the sphere. Is there any chance could you please improve that?
Link | Replychristian 4 years, 7 months ago
Thank you for your comment: there's a great article about the north magnetic pole ("dip pole") vs the north geomagnetic pole ("dipole") here: https://www.scientificamerican.com/article/the-earth-has-more-than-one-north-pole/
Link | ReplyThe streamlines are plotted according to Matplotlib's own algorithm and where they converge some tend to get dropped. I think the overall impression is clear enough, though.
pilis 4 years, 6 months ago
If I have an electric field that has E_r and E_theta components but E_phi = 0 (the potential has azimuthal symmetry), can it be plotted in the same way?
Link | ReplyWhy graph it in x and y but not in x and z for example? Why does theta become the azimuthall angle?
(Srry for my English)
Thx :D
pilis 4 years, 6 months ago
Why did you change spherical coordinates to polar?
Link | Replychristian 4 years, 6 months ago
I used polar coordinates because of the cylindrical symmetry: once you agree that the azimuthal component of the magnetic field (expressed in spherical polar coordinates) is constant, then it's really a two-dimensional problem with coordinates r and theta. It doesn't matter much how you choose to label the Cartesian plane that these coordinates are transformed onto. I chose (x, y) where, unfortunately, y coincided with the old x (hence North pointed to the right) and x with the old z (hence the azimuthal / polar confusion). I think I might choose differently if I did it again...
Link | ReplyNew Comment