The Weierstrass function

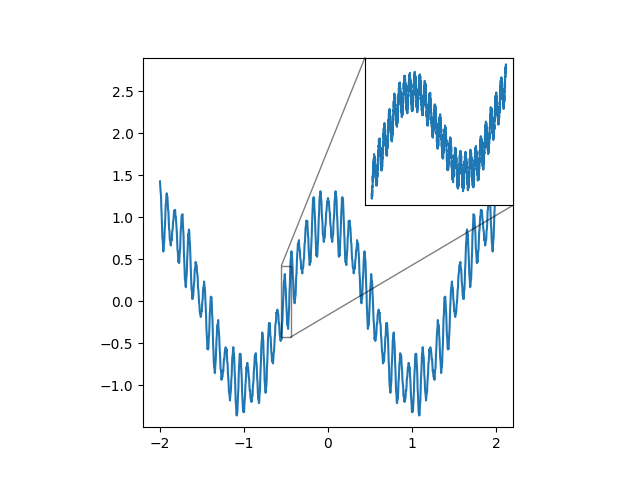
import numpy as np
import matplotlib.pyplot as plt

# Number of points to plot.
N = 1000
# Parameters of this particular Weierstrass function, f(x).
# b must be an odd integer and 0 < a < 1.
a, b = 0.3, 23
# The condition for f(x) to be continuous but nowhere differentiable:
assert a*b > 1 + 3 * np.pi / 2

def get_W(x, f=0, nterms=50):
    """Return the Weierstrass function at x."""
    for k in range(nterms):
        term = a**k * np.cos(b**k * np.pi * x)
        f += term
    return f

def get_f(Dx, cx=0, nterms=50):
    """
    Return the Weierstrass function on the interval [-Dx/2, Dx/2], centered
    at cx, using nterms to approximate the infinite sum. x can be an array.

    """

    x = np.linspace(cx - Dx / 2, cx + Dx / 2, N)
    f = np.zeros(N)
    f = get_W(x, f, nterms)
    return x, f

# The "outside" plot.
Dx = 4
x, y = get_f(Dx)
fig, ax = plt.subplots()
ax.plot(x, y)
ax.axis('square')

# The inset plot.
axin = ax.inset_axes([0.6, 0.6, 0.4, 0.4])
Dx_in, cx_in = 0.1, -0.5
xin, yin = get_f(Dx_in, cx_in)
axin.plot(xin, yin)
axin.set_xticks([])
axin.set_yticks([])
ax.indicate_inset_zoom(axin, edgecolor="black")

plt.show()