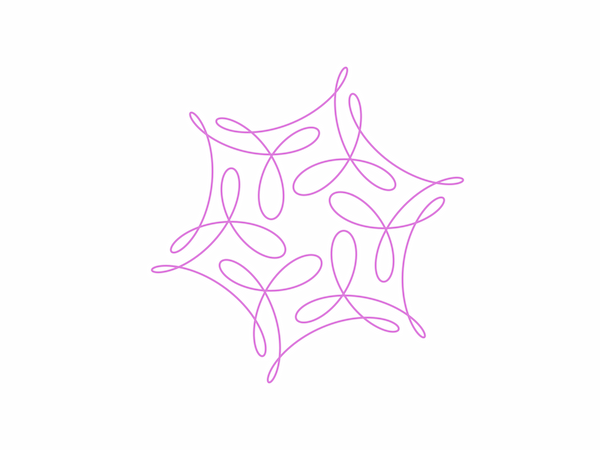
The "Mystery Curve"

import sys
import matplotlib.pyplot as plt
import numpy as np

def f(t, k):
    """Return the "Mystery Curve" for parameter k on a grid of t values."""

    def P(z):
        return 1 - z / 2 - 1 / z**3 / 3j
    return np.exp(1j*t) * P(np.exp(k*1j*t))

# k is supplied as a command line argument.
k = int(sys.argv[1])

# Choose a grid of t values at a suitable resolution so that the curve.
# is well-represented.
t = np.linspace(0, 2*np.pi, 200*k+1);

u = f(t, k)

# Plot the Mystery Curve in a pleasing colour, removing the axis clutter.
fig, ax = plt.subplots(facecolor='w')
ax.plot(np.real(u), np.imag(u), lw=2, color='m', alpha=0.5)
ax.set_aspect('equal')
plt.axis('off')

plt.savefig('mystery_curve_{}.png'.format(k))
plt.show()