The Möbius function and the Mertens conjecture
Posted on 25 January 2020
This blog post was inspired by Holly Krieger's video for Numberphile.
The Möbius function, $\mu(n)$, is related to the factorization of the positive integer $n$ through $$ \mu(n) = \delta_{\Omega(n), \omega(n)} (-1)^{\Omega(n)}, $$ where $\Omega(n)$ is the number of prime factors of $n$, $\omega(n)$ is the number of distinct prime factors of $n$, and $\delta_{i,j}$ is the Kronecker delta function (equal to 1 or 0 according to whether $i=j$ or not).
That is, $\mu(n) = 1$ if $n$ is a square-free and has an even number of factors, $\mu(n) = -1$ if $n$ is a square-free and has an odd number of factors, and $\mu(n) = 0$ if $n$ has a repeated prime factor. For example,
| $n$ | Factorization | $\mu(n)$ |
|---|---|---|
| 1 | $1$ | |
| 2 | = $2$ | $-1$ |
| 3 | = $3$ | $-1$ |
| 4 | = $2^2$ | $0$ |
| 5 | = $5$ | $-1$ |
| 6 | = $2\cdot 3$ | $1$ |
| 7 | = $7$ | $-1$ |
| 8 | = $2^3$ | $0$ |
| 9 | = $3^2$ | $0$ |
| 10 | = $2\cdot 5$ | $1$ |
| 11 | = $11$ | $-1$ |
| 12 | = $2^2\cdot 3$ | $0$ |
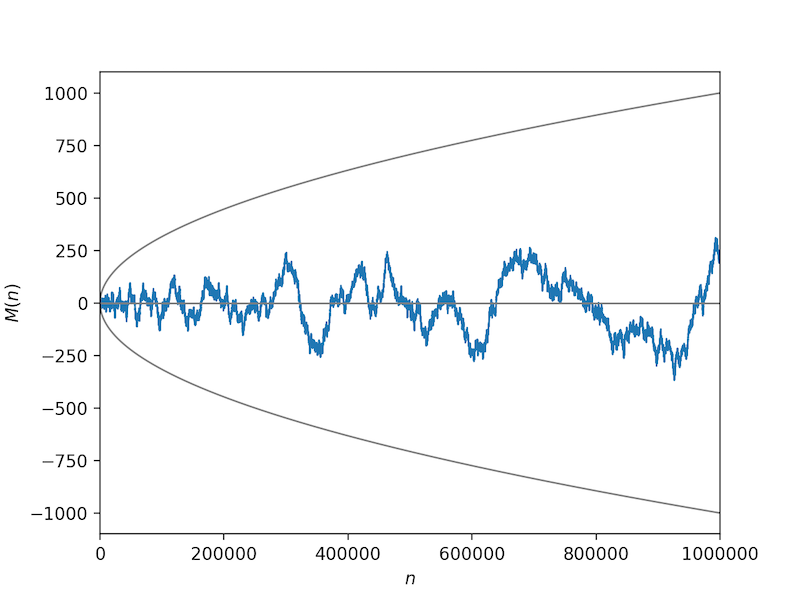
The Mertens function is the cumulative sum of the Möbius function: $$ M(n) = \sum_{k=1}^n \mu(k). $$
This function is the subject of a famous disproven conjecture: that the magnitude of $M(n)$ is always less than the square root of $n$: $$ |M(n)| < \sqrt{n} \quad\quad(not\;true) $$ It was disproved by Andrew Odlyzko and Herman te Riele in 1985; the current upper-bound to a counter-example was shown by Kotnik and Te Riele (2006) to be below $10^{6.91\times 10^{39}}$, but the precise value is not known.
The code below plots the Mertens function and $\pm \sqrt{n}$ for $n \le 10^6$.
import numpy as np
import matplotlib.pyplot as plt
NMAX = 1000000
def get_mu_seq(nmax):
"""Return the values of the Möbius function up to nmax in a list."""
sqrt_nmax = int(np.sqrt(nmax))
mu = [1] * (nmax+1)
# Comopose the numbers from their factors, keeping track of the
# parity of the number of factors in the sign. If a number is the
# product of two prime factors set its value of mu to 0.
for k in range(2, sqrt_nmax+1):
if mu[k] == 1:
for j in range(k, nmax+1, k):
mu[j] *= -k
for j in range(k*k, nmax+1, k*k):
mu[j] = 0
# Set the value of the Möbius function according to the value in mu.
for k in range(2, nmax+1):
if mu[k] == k:
mu[k] = 1
elif mu[k] == -k:
mu[k] = -1
elif mu[k] < 0:
mu[k] = 1
elif mu[k] > 0:
mu[k] = -1
return mu
mu = get_mu_seq(NMAX)
n = range(1,NMAX+1)
# Plot the Mertens function and its (wrongly) conjectured bounds, ±sqrt(n).
plt.plot(n, np.cumsum(mu[1:]), lw=1)
plt.plot(n, np.sqrt(n), '0.5', lw=1)
plt.plot(n, -np.sqrt(n), '0.5', lw=1)
plt.xlim(0,NMAX+1)
plt.axhline(0, 0, NMAX+1, c='0.5', lw=1)
plt.xlabel('$n$')
plt.ylabel('$M(n)$')
plt.show()