The harmonically-driven pendulum

Posted by: christian on 25 Jul 2017

(0 comments)

For the purposes of this article, the harmonically-driven pendulum is one whose anchor point moves in time according to $x_0(t) = A\cos\omega t$. As with previous posts, the position of the pendulum bob with time can be described using Lagrangian mechanics. In a coordinate system with the pendulum anchor initially at $(0,0)$ and the $y$-axis pointing up, the components of the bob position and velocity as a function of time are:

\begin{align*} x &= l\sin\theta + A\cos\omega t& \dot{x} &= l\dot{\theta}\cos\theta - A\omega\sin\omega t\\ y &= -l\cos\theta & \dot{y} &= l\dot{\theta}\sin\theta \end{align*}

The kinetic energy, $T = \tfrac{1}{2}m(\dot{x}^2 + \dot{y}^2)$, and potential energy, $V = mgy$ then give the Lagrangian, $\mathcal{L} = T - V$ as

\begin{align*} \mathcal{L} = T - V = \tfrac{1}{2}m(l^2\dot{\theta}^2 + A^2\omega^2\sin^2\omega t - 2A\omega l \dot{\theta}\sin\omega t\cos\theta) + mgl\cos\theta, \end{align*}

and the Euler-Lagrange equation leads to the following equation of motion:

\begin{align*} \ddot{\theta} = \frac{A\omega^2}{l}\cos\omega t - \frac{g}{l}\sin\theta. \end{align*}

This equation cannot be solved analytically, but in the limit of small $\theta$ it reduces to the second-order non-homogeneous differential equation:

$$ \ddot{\theta} \approx \frac{A\omega^2}{l}\cos\omega t - \frac{g}{l}\theta $$

which may be solved by standard methods to give

$$ \theta_\mathrm{approx} = \frac{A\omega^2}{l(\omega_0^2-\omega^2)}(\cos\omega t - \cos\omega_0 t), $$

for the simplest initial conditions, $\theta(0) = \dot{\theta}(0) = 0$, where $\omega_0 = \sqrt{g/l}$ is the pendulum's "natural" frequency.

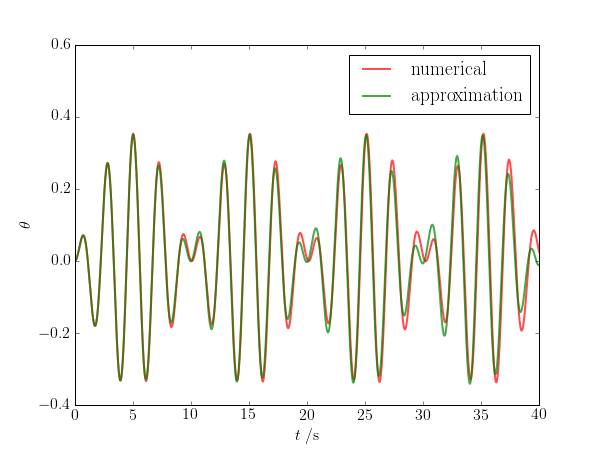
Here is a plot of both $\theta(t)$ and $\theta_\mathrm{approx}(t)$ for a small driving amplitude, $A$. Because of resonance (when $\omega \approx \omega_0$), even a small $A$ is not guaranteed to keep $\theta$ small enough for the approximate formula to hold indefinitely.

enter image description here

enter image description here

Here is the Python code. As before, the frames of the animation are placed in a directory frames/.

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.patches import Circle

# Pendulum rod length (m), drive frequency (s-1), amplitude (m), mass (kg)
L, w, A, m = 1, 2.5, 0.1, 1
# The gravitational acceleration (m.s-2).
g = 9.81

def deriv(y, t, L, w, A, m):
    """Return the first derivatives of y = theta, z1, L, z2."""
    theta, thetadot = y

    dtheta_dt = thetadot
    dthetadot_dt = (A * w**2 / L * np.cos(w*t) * np.cos(theta) -
                   g * np.sin(theta))
    return dtheta_dt, dthetadot_dt

# Maximum time, time point spacings and the time grid (all in s).
tmax, dt = 40, 0.01
t = np.arange(0, tmax+dt, dt)
# Initial conditions: theta, dtheta/dt
y0 = [0, 0]

# Do the numerical integration of the equations of motion
y = odeint(deriv, y0, t, args=(L, w, A, m))
# Unpack theta and thetadot as a function of time
theta, thetadot = y[:,0], y[:,1]

# Convert to Cartesian coordinates of the two bob positions.
x = L * np.sin(theta)
y = -L * np.cos(theta)

# Plotted bob circle radius
r = 0.05
# Plot a trail of the m2 bob's position for the last trail_secs seconds.
trail_secs = 1
# This corresponds to max_trail time points.
max_trail = int(trail_secs / dt)

def make_plot(i):
    """
    Plot and save an image of the spring pendulum configuration for time
    point i.

    """

    x0 = A * np.cos(w * t[i])
    plt.plot([x0, x0+x[i]], [0, y[i]])
    # Circles representing the anchor point of rod 1 and the bobs
    c0 = Circle((x0, 0), r/2, fc='k', zorder=10)
    c1 = Circle((x0+x[i], y[i]), r, fc='r', ec='r', zorder=10)
    ax.add_patch(c0)
    ax.add_patch(c1)

    # The trail will be divided into ns segments and plotted as a fading line.
    ns = 20
    s = max_trail // ns

    for j in range(ns):
        imin = i - (ns-j)*s
        if imin < 0:
            continue
        imax = imin + s + 1
        # The fading looks better if we square the fractional length along the
        # trail.
        alpha = (j/ns)**2
        ax.plot(x0+x[imin:imax], y[imin:imax], c='r', solid_capstyle='butt',
                lw=2, alpha=alpha)

    # Centre the image on the fixed anchor point, and ensure the axes are equal
    ax.set_xlim(-np.max(L)-r-A, np.max(L)+r+A)
    ax.set_ylim(-np.max(L)-r-A, np.max(L)+r+A)
    ax.set_aspect('equal', adjustable='box')
    plt.axis('off')
    plt.savefig('frames/_img{:04d}.png'.format(i//di), dpi=72)
    # Clear the Axes ready for the next image.
    plt.cla()

fig = plt.figure(figsize=(8.33333333, 6.25), dpi=72)
ax = fig.add_subplot(111)
ax.plot(t, theta, lw=2, c='r', alpha=0.7, label='numerical')

# Approximate solution of the ODE for small theta.
w0 = np.sqrt(g/L)
theta_approx = A*w**2/L/(w0**2-w**2)*(np.cos(w*t) - np.cos(w0*t))
ax.plot(t, theta_approx, lw=2, c='g', alpha=0.7, label='approximation')

ax.set_xlabel(r'$t\;/\mathrm{s}$')
ax.set_ylabel(r'$\theta$')
ax.set_xlim(0,tmax)
ax.set_ylim(-0.4, 0.6)
ax.legend()
plt.savefig('driven-theta.png', dpi=72)
plt.show()

# Make an image every di time points, corresponding to a frame rate of fps
# frames per second.
# Frame rate, s-1
fps = 10
di = int(1/fps/dt)
# This figure size (inches) and dpi give an image of 600x450 pixels.
fig = plt.figure(figsize=(8.33333333, 6.25), dpi=72)
ax = fig.add_subplot(111)

for i in range(0, t.size, di):
    print(i // di, '/', t.size // di)
    make_plot(i)
Current rating: 4.1

Comments

Comments are pre-moderated. Please be patient and your comment will appear soon.

There are currently no comments

New Comment

required

required (not published)

optional

required