The Goat Problem

Posted by: christian on 29 Dec 2022

(0 comments)

A goat is tethered on the perimeter of a circular paddock of grass by a rope of length $r$. What should $r$ be to allow the goat to graze on a maximum of half the area of the paddock?

This is a famous problem in recreational mathematics and is usually solved by approximate or numerical methods, despite being relatively easy to express in the form of a mathematical equation (derived below). The mathematician Ingo Ullisch recently derived an exact solution as the cosine of the ratio of two contour integrals, which has been (generously) described as being in closed-form:

$$ r = 2 \cos\left(\frac{1}{2} \frac{\oint_{|z - 3 \pi / 8| = \pi / 4} z / (\sin z - z \cos z - \pi / 2) \,dz}{\oint_{|z - 3 \pi / 8| = \pi / 4} 1 / (\sin z - z \cos z - \pi / 2)\, dz}\right). $$

Here we will take the numerical solution approach. Let the paddock be a unit circle, with area $\pi$, centred at O, and tether the goat at point T. The extent of the goat's grazing area is ilustrated below. Our job is to find the value of $r$ that makes this area equal to $\pi/2$.

First note a few relations that will prove useful:

\begin{align} (1)\quad &\alpha = \pi - 2\theta\\ (2)\quad &\sin\theta = \frac{\sin\alpha}{r}\\ (3)\quad &r^2 = 1 + 1 - 2\cos\alpha = 2(1-\cos\alpha)\\ (4)\quad &1 = 1+r^2 -2r\cos\theta \Rightarrow \theta = \arccos\left(\frac{r}{2}\right) \end{align}

The second of these is the sine rule for triangles; the third and forth follow from the cosine rule.

The area of the circular sector TPQ is:

$$ A_1 = \pi r^2 \frac{\theta}{2\pi} = \frac{r^2\theta}{2}, $$

the area of the circular sector OTP is:

$$ A_2 = \pi\frac{\alpha}{2\pi} = \frac{\alpha}{2} $$

and the area of the triangle OTP is:

$$ A_3 = \frac{1}{2}r\sin\theta = \frac{1}{2}\sin\alpha, $$

using the result (2).

The area that the goat has to graze in is therefore $A = 2(A_1 + A_2 - A_3)$ and the problem is to solve

$$ A = r^2\theta + \alpha - \sin\alpha = \frac{\pi}{2} $$

for $\alpha$ and hence $r$. Using (1) to write $\theta = \frac{1}{2}(\pi - \alpha)$ and rearranging yields:

$$ \sin\alpha + (\pi - \alpha)\cos\alpha = \frac{\pi}{2}. $$

This equation is readily solved using, for example, the Newton–Raphson root-finding algorithm, as implemented by scipy.optimize.newton:

import numpy as np
from scipy.optimize import newton

def func(alpha):
    return np.sin(alpha) + (np.pi - alpha) * np.cos(alpha) - np.pi / 2

theta_guess = np.pi / 2
alpha = newton(func, theta_guess)
print(alpha)

1.2358969242799094

This value for $\alpha$ is in radians. The corresponding rope-length, $r$ is given, from (3) as:

r = np.sqrt(2 * (1-np.cos(alpha)))
print(r)

1.1587284730181215

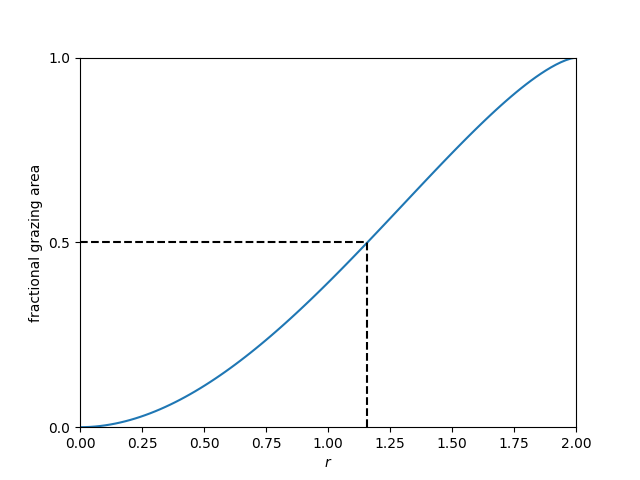
The variation of the grazable fraction of the paddock, $A/\pi$ as a function of the rope length, $r$, can be plotted as follows:

import matplotlib.pyplot as plt

rgrid = np.linspace(0, 2, 100)
cos_alpha = 1 - rgrid**2 / 2
alpha = np.arccos(cos_alpha)
theta = (np.pi - alpha) / 2
A = rgrid**2 * theta + alpha - np.sin(alpha)
r = 1.1587284730181215

plt.plot(rgrid, A / np.pi)
plt.hlines(0.5, 0, r, colors='k', linestyles='--')
plt.vlines(r, 0, 0.5, colors='k', linestyles='--')
plt.xlim(0, 2)
plt.ylim(0, 1)
plt.yticks([0, 0.5, 1])
plt.xlabel('$r$')
plt.ylabel('fractional grazing area')
plt.show()

• ← Maurer Roses
• Modular arithmetic on a circle →