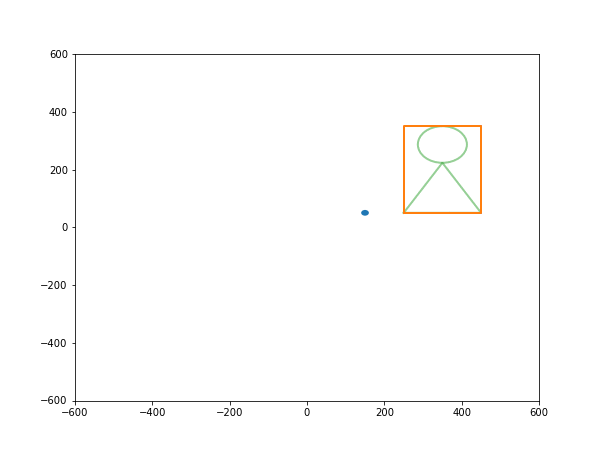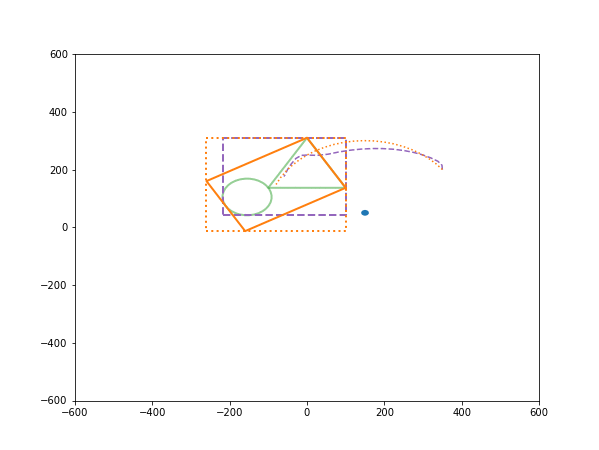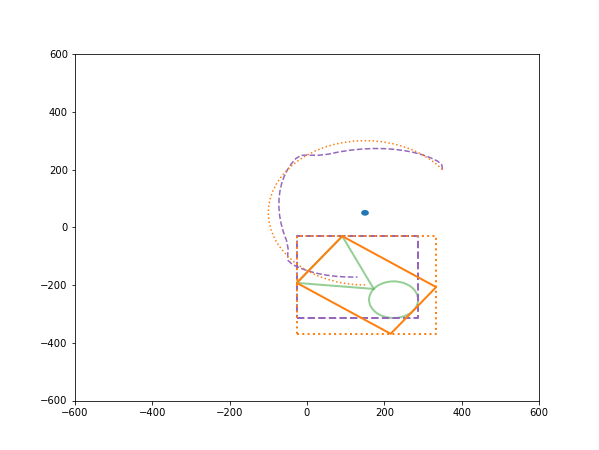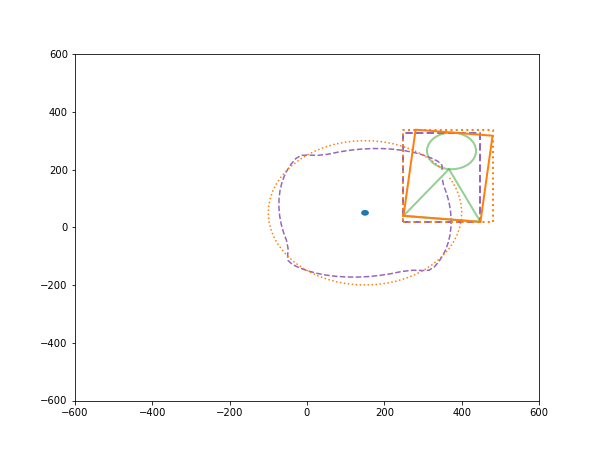
The following code plots a two-dimensional object and its bounding box for several rotations about an arbitrary point. Three types of bounding box are considered: (1) the original bounding box, rotated by the same amount as the object, (2) the bounding box to that bounding box (such that its sides remain parallel to the axes), and (3) the bounding box to the rotated object with sides parallel to the axes).

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle
DPI = 72

# Rotation centre. It is helpful to have this with shape (2,1)
cx, cy = 150, 50
rc = np.array(((cx, cy),)).T

# Initial width and height of the bounding rectangle we will fit the object in.
rw, rh = 200, 300
# Initial corner positions of the bounding rectangle 
x1, y1, x2, y2 = 250, 50, 250+rw, 50+rh

def rotate_points(pts, theta, rc):
    """Rotate the (x,y) points pts by angle theta about centre rc."""
    c, s = np.cos(theta), np.sin(theta)
    R = np.array(((c,-s), (s, c)))
    return rc + R @ (pts - rc)


def plot_poly(pts, colour='tab:blue', lw=2, opacity=1, ls='-'):
    """Plot a closed polygon with vertices at pts."""

    plot_pts = np.vstack((pts.T, pts[:,0]))
    ax.plot(*zip(*plot_pts), c=colour, lw=lw, alpha=opacity, ls=ls)


def plot_obj(pts, colour='tab:green', lw=2):
    """Draw the object we are rotating: a circle and polygon."""

    plot_poly(pts[:,1:], colour, lw=lw, opacity=0.5)
    circle = Circle(pts[:,0], obj_cr, edgecolor=colour, fill=False, lw=lw,
                    alpha=0.5)
    ax.add_patch(circle)


def get_boundary_pts(pts):
    """Get the vertices of the bounding rectangle for the points pts."""

    xmin, xmax = np.min(pts[0]), np.max(pts[0])
    ymin, ymax = np.min(pts[1]), np.max(pts[1])
    return np.array(((xmin,ymin), (xmax,ymin), (xmax, ymax), (xmin, ymax))).T


def get_obj_boundary(obj_pts):
    """Get the vertices of the bounding rectangle for the rotated object."""

    fcx, fcy = obj_pts[:,0]
    # Get the boundary from the triangle coordinates and the circle limits
    _obj_boundary = np.vstack((obj_pts.T[1:], (fcx-obj_cr, fcy),
                (fcx+obj_cr, fcy), (fcx, fcy-obj_cr), (fcx, fcy+obj_cr))).T
    return get_boundary_pts(_obj_boundary)


fig, ax = plt.subplots(figsize=(8.33333333, 8.33333333), dpi=DPI)

# Initial bounding rectangle of unrotated object.
pts = np.array( ((x1,y1), (x2,y1), (x2,y2), (x1,y2)) ).T
# The radius of the circle in our plotted object.
obj_cr = (rh - rw*np.sqrt(3)/2)/2
# The coordinates defining our object.
obj_pts = np.array( ((x1 + rw/2, y1 + rh - obj_cr),    # circle centre
                     (x1, y1), (x2, y1),               #
                     (x1+rw/2, y2-2*obj_cr),           # triangle
                    )).T
# Plot the unrotated object and its bounding rectangle
plot_obj(obj_pts)
plot_poly(pts)

nrots = 60
theta = np.radians(360 // nrots)
boundary_trail_pts, obj_boundary_trail_pts = [], []
for i in range(nrots):
    fig, ax = plt.subplots(figsize=(8.33333333, 6.25), dpi=DPI)
    ax.set_xlim(-600,600)
    ax.set_ylim(-600,600)
    # Indicate the centre of rotation
    ax.add_patch(Circle((cx,cy), 10))

    # Plot the object
    plot_obj(obj_pts)
    # Plot the rotated object's boundary
    boundary_pts = get_obj_boundary(obj_pts)
    plot_poly(boundary_pts, colour='tab:purple', ls='--')
    obj_boundary_trail_pts.append(np.mean(boundary_pts, axis=1))
    ax.plot(*zip(*obj_boundary_trail_pts), c='tab:purple', ls='--')

    # Plot the original boundary, rotated
    plot_poly(pts, colour='tab:orange')
    # Plot the boundary to the original rotated boundary
    boundary_pts = get_boundary_pts(pts)
    plot_poly(boundary_pts, colour='tab:orange', ls=':')
    boundary_trail_pts.append(np.mean(boundary_pts, axis=1))
    ax.plot(*zip(*boundary_trail_pts), c='tab:orange', ls=':')

    plt.savefig('frames/bbrot-{:03d}.png'.format(i+1), dpi=DPI)

    obj_pts = rotate_points(obj_pts, theta, rc)
    pts = rotate_points(pts, theta, rc)
    plt.close(fig)