The Babylonian spiral
Posted on 22 May 2020
A Babyonian spiral (OEIS A256111) is the figure formed by starting with a zero-vector at the origin and concatenating vectors such that each subsequent vector is the next one longer than the previous one that also lands on a position with integral Cartesian coordinates. That is, the $i$th vector has integer components $x_i$ and $y_i$ satisfying, $x_i^2 + y_i^2 = n_i^2 > n_{i-1}^2$. Each vector is chosen such that it minimizes the angular separation from the previous one.
The algorithm produces a shape that starts off resembling a (slightly wonky) spiral:
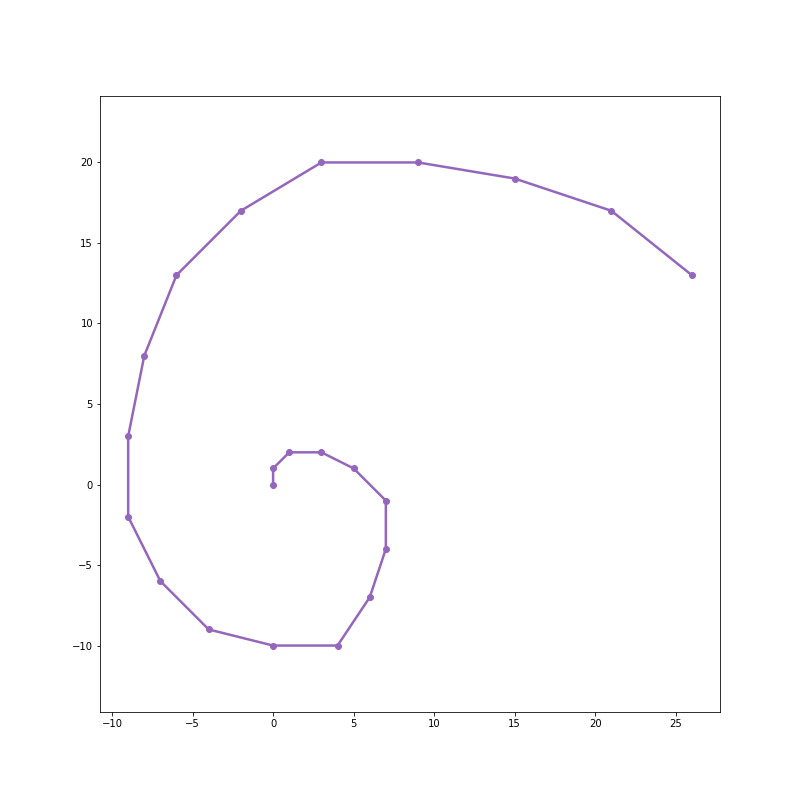
After 40 steps, things are beginning to look shaky:
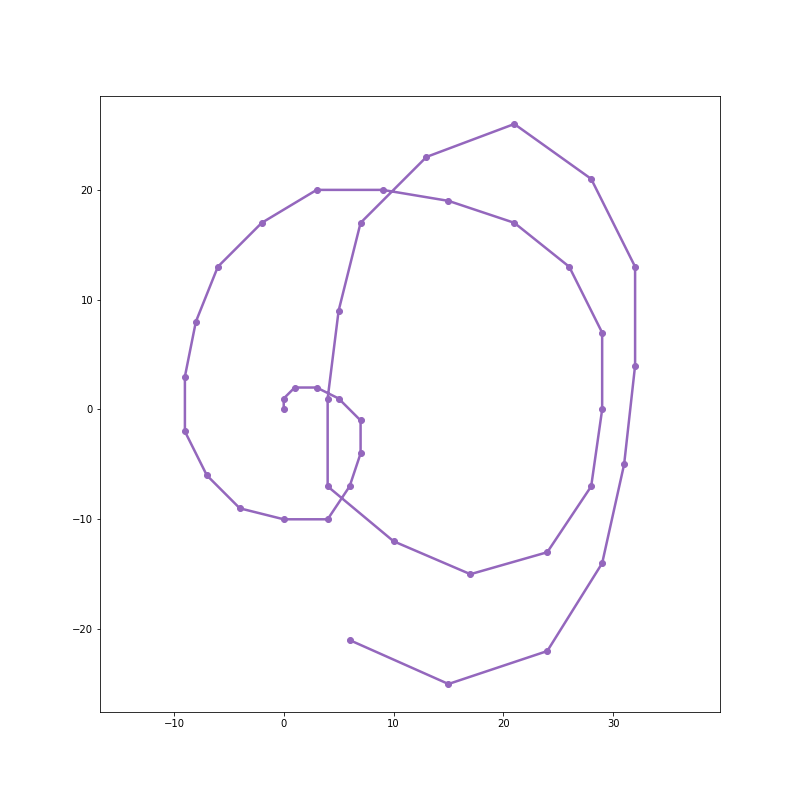
After 200 steps:
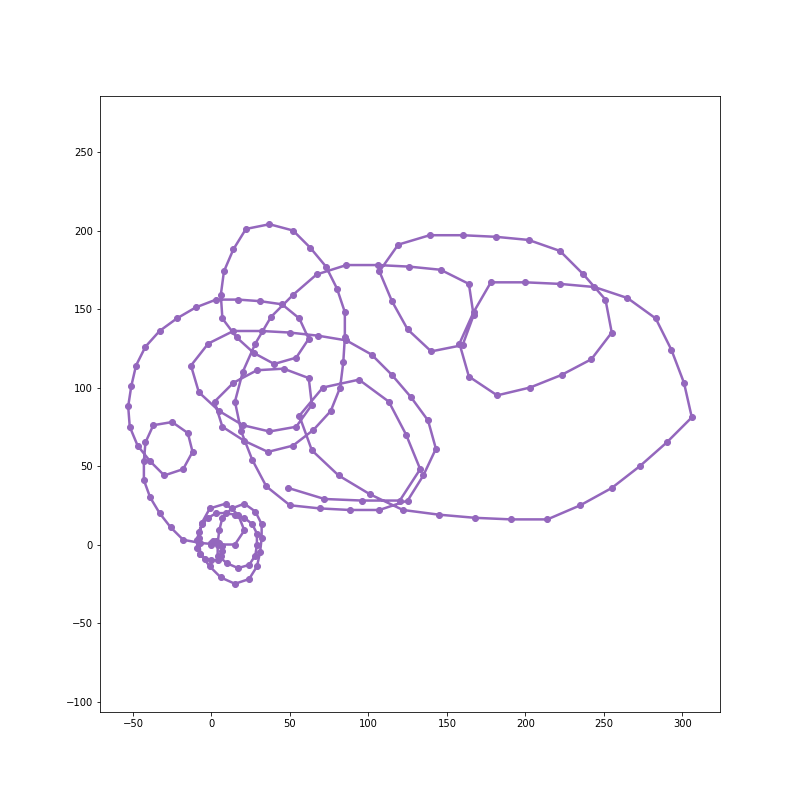
By 2000 steps, it resembles a scribble:
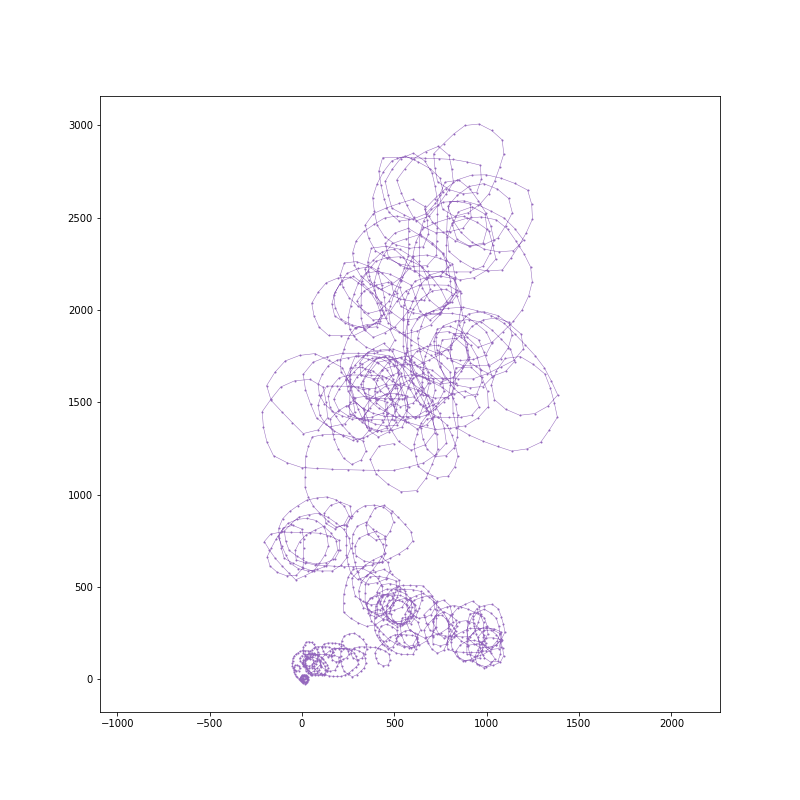
20000 steps:
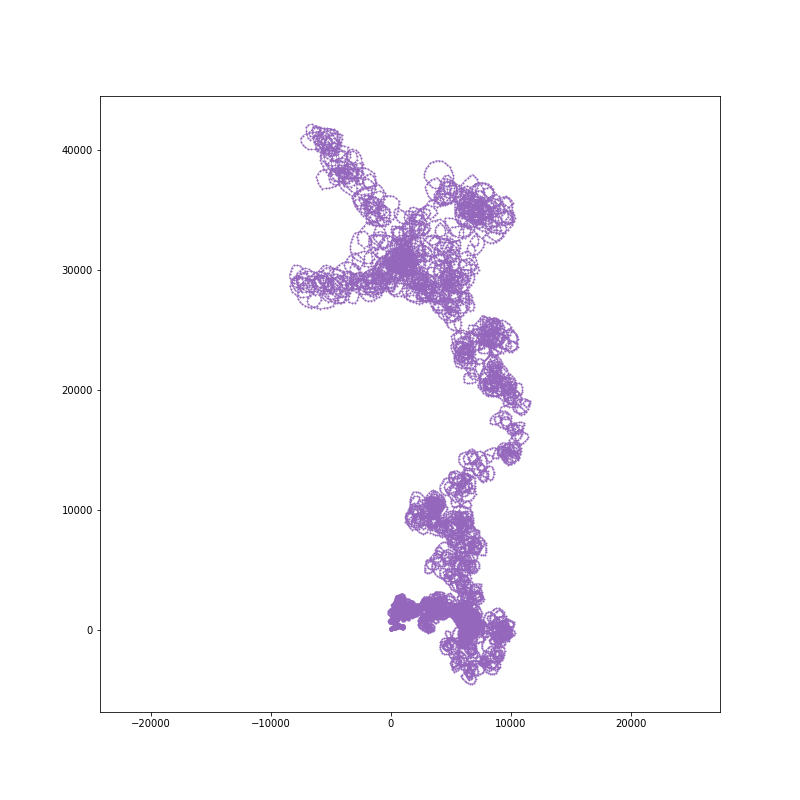
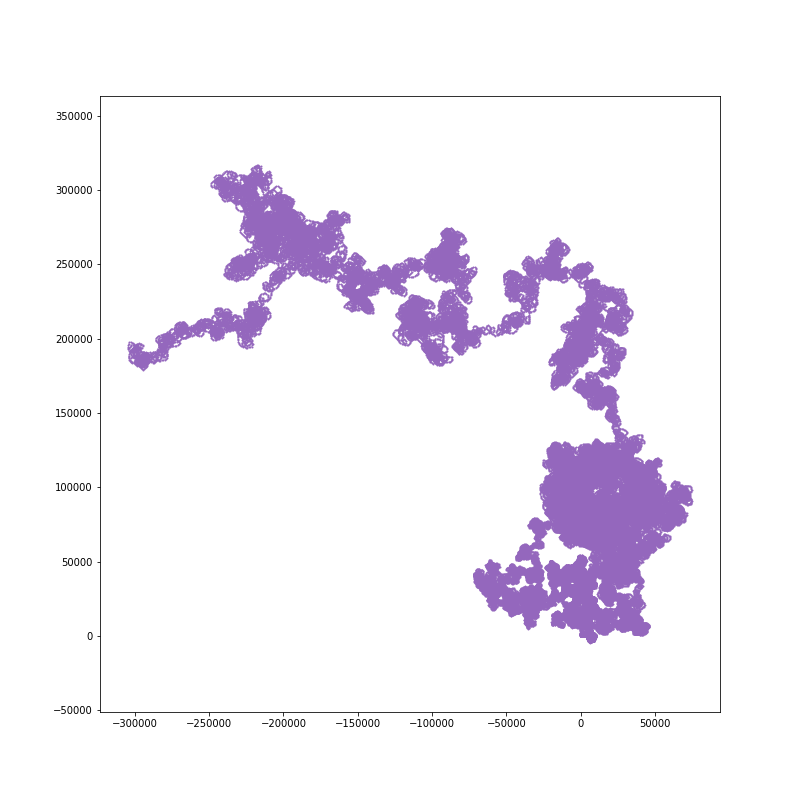
200000 steps:
The Python code below produces these figures (alter the variable nsteps and, possibly, the plot line width and marker size).
import sys
import math
import time
import matplotlib.pyplot as plt
nsteps = 2000
# Cache the first CACHE_NMAX square numbers.
CACHE_NMAX = 1000
squares = [a**2 for a in range(CACHE_NMAX+1)]
def get_pairs(n2):
"""Find all pairs of integers ia and ib such that ia^2 + ib^2 = n2."""
pairs = []
# Index into the list of squares with ia <= ib to find values
# a = ia**2, b = ib**2 satisfying a + b == n2. Increase ia up to
# the square root of n2 and, for each value of ia, decrease ib from the
# square root of n2 until a + b < n2.
ia = 0
ib = int(math.sqrt(n2)) + 1
if ib > CACHE_NMAX:
sys.exit('Size of squared numbers cache, CACHE_NMAX = {}, exceeded.'
.format(CACHE_NMAX))
while True:
a = squares[ia]
if a > n2 // 2:
break
while True:
b = squares[ib]
if a + b < n2:
break
elif a + b == n2:
# add all possible orientations for a vector of this length
# to land on a lattice point.
pairs.extend([(ia, ib), (-ia, ib), (ia, -ib), (-ia, -ib),
(ib, ia), (ib, -ia), (-ib, ia), (-ib, -ia)])
ib -= 1
ia += 1
return set(pairs)
def get_vecs(nsteps):
"""Get the vectors forming the Babylonian spiral up to nsteps steps."""
# Start at the origin; the first step is to (0, 1).
vecs = [(0, 0), (0, 1)]
n2 = 1
for step in range(nsteps):
# The previous vector and its angle.
x0, y0 = vecs[-1]
theta = math.atan2(y0, x0)
# Find the next set of candidate vectors longer than (x0, y0) that
# land on a lattice point.
pairs = []
while not pairs:
n2 += 1
pairs = get_pairs(n2)
# Pick the new vector with the smallest (clockwise) angular deviation
# from the previous one.
x1, y1 = min(pairs,
key=lambda v: (theta - math.atan2(v[1], v[0])) % math.tau)
vecs.append((x1, y1))
return vecs
def get_pos(nsteps):
"""Get the positions of points on the Babylonian spiral up to nsteps."""
vecs = get_vecs(nsteps)
# Start at the origin and add on subsequent vectors, one at a time.
pos = [vecs[0]]
x, y = pos[0]
for i in range(1, len(vecs)):
x, y = vecs[i][0] + x, vecs[i][1] + y
pos.append((x, y))
return pos
start = time.time()
pos = get_pos(nsteps)
end = time.time()
print('Time taken: {:g} s'.format(end - start))
DPI = 72
fig, ax = plt.subplots(figsize=(800 / DPI, 800 / DPI), dpi=DPI)
plt.plot(*zip(*pos), lw=0.5, c='tab:purple', marker='.', ms=2)
plt.axis('equal')
plt.savefig('babylonian-spiral-{}.png'.format(nsteps), dpi=DPI)
plt.show()