The arcsine law

Posted by: christian on 15 Feb 2017

(0 comments)

Suppose a fair coin is tossed $N$ times and the number of "heads", $n_\mathrm{heads}$, and "tails", $n_\mathrm{tails}$, recorded after each toss. Over the course of the trial, how many times is the number of heads recorded greater than the number of tails? Naive intuition might lead to the expectation that as $N$ increases the number of times "heads" is in the lead increases in proportion.

In fact, the number of changes of "lead" increases only as $\sqrt{N}$: that is, the time between "equalization" of $n_\mathrm{heads}$ and $n_\mathrm{tails}$ becomes longer and longer as $N$ increases. Once one player begins to win, they are likely to stay ahead.

The simple simulation of the coin-tossing experiment as a random walk given below illustrates the problem.

The code on this page is also available on my github page.

import numpy as np
import matplotlib.pylab as plt

def coin_tosses(ntosses):
    return np.cumsum(np.random.choice([-1,1], size=ntosses))

ntrials = 10
ntosses = 1000

for i in range(ntrials):
    plt.plot(range(ntosses), coin_tosses(ntosses), c='r', alpha=0.4)
plt.axhline(c='k')
plt.xlabel('Toss number')
plt.ylabel(r'$n_\mathrm{heads}-n_\mathrm{tails}$')
plt.savefig('random_walk.png')
plt.show()

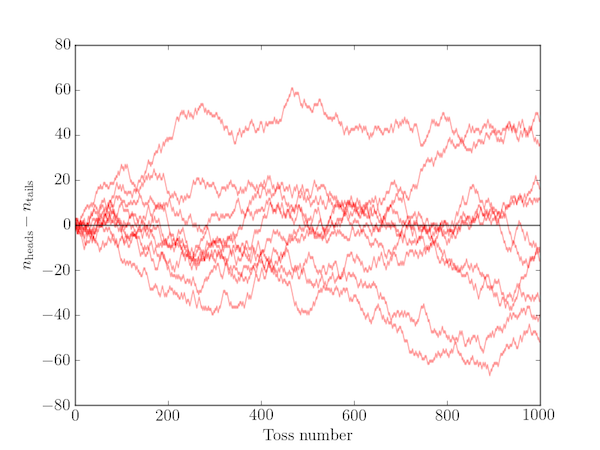
From the simulated trials shown above, it certainly seems plausible that the number of times the red line crosses the $x-$axis (i.e. the lead swaps) does not increase in proportion to the number of coin tosses. In fact, the probability of there being exactly $r$ changes out of $N$ tosses falls monotonically as $r$ increases from 0: that is, the most likely outcome is that the lead never swaps at all.

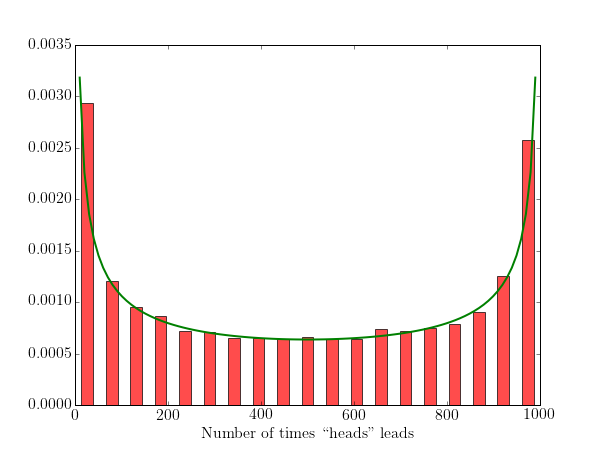
A more quantitative approach to this problem was described by William Feller[1] who derived the following probability distribution for the proportion of times that heads (or, equivalently of course, tails) will lead: $$ P\left(\frac{n_\mathrm{heads}}{n_\mathrm{tosses}} < x \right) = \frac{1}{\pi} \int_0^x \frac{1}{\sqrt{u(1-u)}}\;\mathrm{d}u = \frac{2}{\pi}\arcsin\sqrt{x}. $$ A somewhat clearer derivation is given by Haggstrom[2].

The code below simulates the coin-tossing experiment and verifies the above distribution for the number of times that heads leads out of 1000 coin tosses.

import numpy as np
import matplotlib.pyplot as plt

# Number of coin tosses in each trial sequence.
ntosses = 1000
# Number of trials of ntosses to repeat.
ntrials = 10000

def coin_tosses(ntosses):
    """Return a running score for ntosses coin tosses.

    Each toss scores +1 for a head and -1 for a tail.

    """

    return np.cumsum(np.random.choice([-1,1], size=ntosses))

def n_times_ahead(ntosses):
    """Return the number of times "heads" leads in N coin tosses.

    Simulate ntosses tosses of a fair coin and return the number of times
    during this sequence that the cumulative number of "heads" results exceeds
    the number of "tails" results.

    """

    tosses = coin_tosses(ntosses)
    return sum(tosses>0)

# Number of tosses out of ntosses that "heads" leads over "tails" for each
# of ntrials trials.
n_ahead = np.array([n_times_ahead(ntosses) for i in range(ntrials)])

# Plot a histogram in nbins bins and the arcsine distribution.
nbins = 20
bins = np.linspace(0, ntosses, nbins)
hist, bin_edges = np.histogram(n_ahead, bins=bins, normed=True)
bin_centres = (bin_edges[:-1] + bin_edges[1:]) / 2

# bar widths in units of the x-axis.
bar_width = ntosses/nbins * 0.5
plt.bar(bin_centres, hist, align='center', width=bar_width, facecolor='r',
        edgecolor=None, alpha=0.7)

# The arcsine distribution
x = np.linspace(0, 1, 100)
plt.plot(x*ntosses, 1/np.pi/np.sqrt(x*(1-x))/ntosses, color='g', lw=2)

plt.xlabel('Number of times ``heads" leads')
plt.savefig('arcsine.png')
plt.show()

1. W. Feller, Introduction to Probability Theory and its Applications, 3rd ed., Wiley (1968).

2. P. Haggstrom, What do schmucks and the arc sine law have in common? (2011)[pdf].

• ← Atomic term symbols
• Interactive particle-in-a-box wavefunctions in Jupyter →