Posted by: christian on 3 Nov 2017
A superellipse (also called a Lamé curve) is the curve described by the equation $$ \left|\frac{x}{a}\right|^p + \left|\frac{y}{b}\right|^p = 1 $$ For $n=2$, this is the equation of an ordinary ellipse and for $a=b=1$ that ellipse is a circle. The corresponding curve for $p=4$ is sometimes called a squircle.
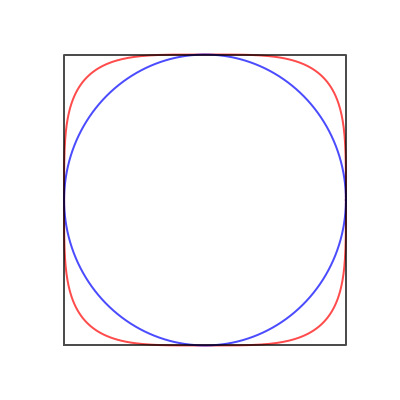
As $p \rightarrow \infty$, the curve approaches the form of a square. The code below plots a few superellipses for $2 \le p \le 25$ and indicates how the area approaches unity as $p$ gets larger. It turns out to be easier to use the parametric representation of the superellipse:
$$ \begin{align*} x(t) &= |\cos t|^{2/n}a\cdot\mathrm{sgn}(\cos t)\\ y(t) &= |\sin t|^{2/n}b\cdot\mathrm{sgn}(\sin t) \end{align*} $$
for $0\le t \le 2\pi$.
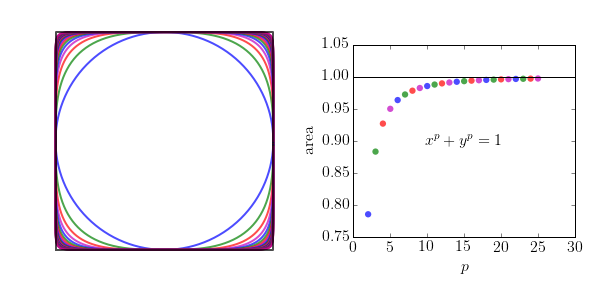
The area of a super ellipse may be written in terms of the gamma function as: $$ A = 4ab\frac{\left[\Gamma\left(1+\frac{1}{n}\right)\right]^2}{\Gamma\left(1+\frac{2}{n}\right)} $$
import numpy as np
from scipy.special import gamma
from matplotlib import rc
import matplotlib.pyplot as plt
from itertools import cycle
# Use LaTeX throughout the figure for consistency
rc('font', **{'family': 'serif', 'serif': ['Computer Modern'], 'size': 16})
rc('text', usetex=True)
# Set up the figure.
dpi = 72
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(600/dpi, 300/dpi), dpi=dpi)
# These are the colours we'll cycle through
colour_cycle = cycle(['b', 'g', 'r', 'm'])
# The parameter t in the parametric description of the superellipse
t = np.linspace(0, 2*np.pi, 500)
# Build an array of values of p up to pmax and assign the corresponding colours
pmax = 26
pvals = np.arange(2, pmax, dtype=int)
colour = [next(colour_cycle) for i in range(pvals.shape[0])]
# All the superellipses will have these plot arguments in common
kwargs = {'lw': 2, 'alpha': 0.7}
# Plot the superellipses
for i,p in enumerate(pvals):
c, s = np.cos(t), np.sin(t)
x = np.abs(c)**(2/p) * np.sign(c)
y = np.abs(s)**(2/p) * np.sign(s)
ax1.plot(x, y, c=colour[i], **kwargs)
# Draw a unit square.
ax1.plot([-1,-1,1,1,-1],[-1,1,1,-1,-1], c='k', **kwargs)
# The x- and y-axes must be scaled the same for circles to look circular.
ax1.axis('equal')
ax1.axis('off')
# Plot the superellipses' areas as a function of p.
ax2.scatter(pvals, gamma(1 + 1/pvals)**2 / gamma(1 + 2/pvals), c=colour,
lw=0, alpha=0.7, s=40)
# Label, annotate and tidy this plot
ax2.set_xlabel(r'$p$')
ax2.set_ylabel('area')
ax2.annotate(s=r'$x^p + y^p = 1$', xy=(0.5, 0.5), xycoords='axes fraction',
ha='center', va='center')
ymin, ymax = ax2.get_ylim()
ax2.set_aspect(pmax / (ymax-ymin))
ax2.axhline(1.0, lw=1, c='k')
fig.tight_layout()
plt.savefig('superellipse.png', dpi=dpi)
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
Peter Panholzer 5 years ago
the word "squircle" was first coined in July 1966 by Peter Panholzer in Toronto, Canada
Link | Replysee
https://www.dynexcorp.com/Squircle_Peter_Panholzer.pdf
Adam D Danz 3 years, 3 months ago
Thanks for walk-through. In case anyone's interested, here's a Matlab version of the code provided by Christian.
Link | Replyt = linspace(0, 2*pi, 500);
pvals = logspace(log10(2),log10(50),10);
clf()
subplot(1,2,1)
clrs = jet(numel(pvals));
colormap(clrs)
hold on
axis equal
grid on
% Draw a unit square.
rectangle('position',[-1 -1 2 2],'LineWidth',2,'LineStyle',':')
for i = 1:numel(pvals)
c = cos(t);
s = sin(t);
x = abs(c).^(2/pvals(i)) .* sign(c);
y = abs(s).^(2/pvals(i)) .* sign(s);
plot (x,y,'-','Color', clrs(i,:), 'LineWidth',1)
end
cb = colorbar();
caxis([min(pvals),max(pvals)])
ylabel(cb,'p')
% Plot the superellipses' areas as a function of p.
subplot(1,2,2)
scatter(pvals, gamma(1 + 1./pvals).^2 ./ gamma(1 + 2./pvals))
% Label, annotate and tidy this plot
xlabel('p')
ylabel('area')
title('x^p + y^p = 1')
yline(1)
axis square
ylim(ylim + [-1,1]*(range(ylim)*.1))
grid on
New Comment