The Spiral of Theodorus (also known as the Snail of Pythogoras), illustrated below, is a well-known visualization of the square roots of the integers as the length of the hypotenuses of a sequence of right triangles, placed edge-to-edge.
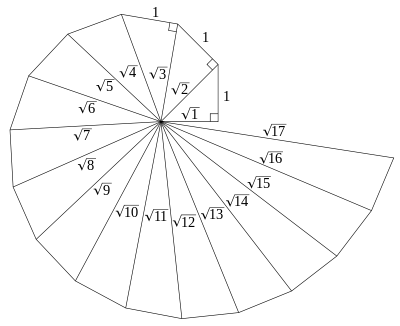The Spiral of Theodorus [Pbroks13 at English Wikipedia: CC-SA-3.0]
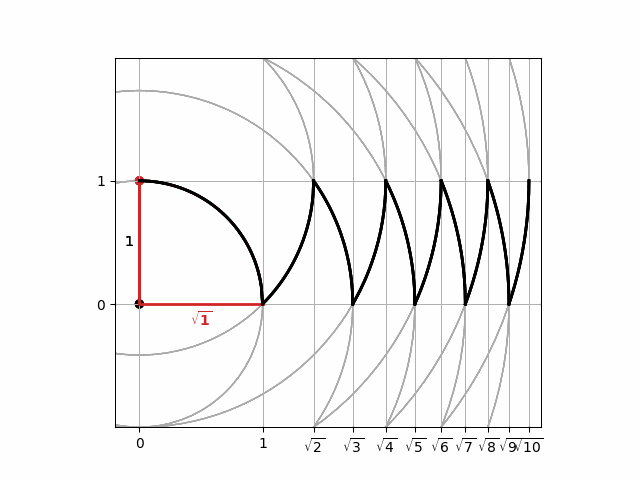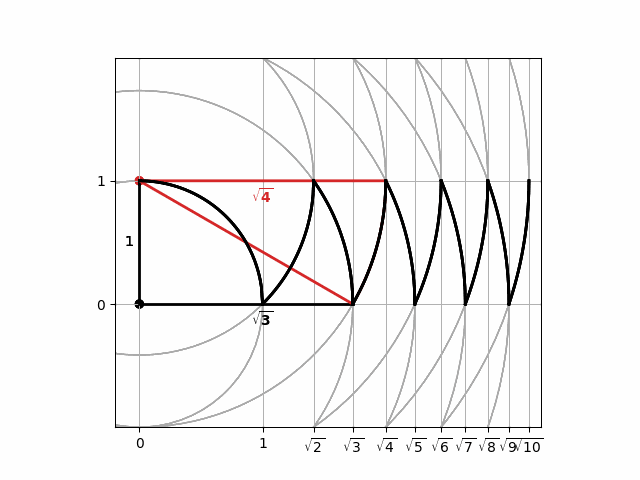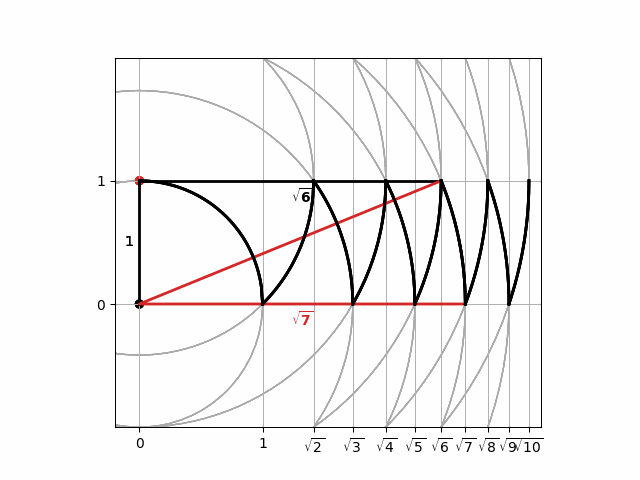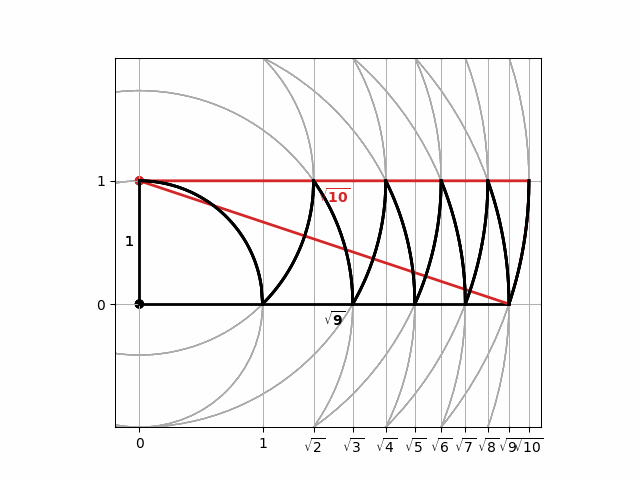
An alternative visualization, highlighted in a recent tweet by user @OLonguet can be used to construct the square roots of the integers using a sequence of circles centred alternateiy on the origin, \((0, 0)\) and on \((0, 1)\). The code below generates an animation of the process, in which the intersection of neighbouring circles resembles a row of shark's teeth.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
PAD = 0.05
def init():
"""Plot the sharks-tooth construction of the square roots of integers.
The position of the (N+1)th tooth is highlighted.
"""
# First draw the circles on alternating centres, (0, 0) and (0, 1).
cy = 0
xmin = 0
for n in range(1, nmax+1):
r = np.sqrt(n)
ax.add_patch(plt.Circle((0, cy), r, fill=None, ec='#aaa'))
xmax = r
x = np.linspace(xmin, xmax, 100)
ax.plot(x, cy + (-1)**cy * np.sqrt(r**2 - x**2), c='k', lw=2)
xmin = r
cy = 1 - cy
# Circle centres: the centre of the circle for tooth N+1 is highlighted in red.
a_pts = ax.scatter([0, 0], [0, 1], s=32, c=['k', 'tab:red'])
ax.text(-PAD, 0.5, '1', ha='right', va='center')
# The radii of the wedge for tooth N+1.
a_p1, = ax.plot([], [], c='k', lw=2)
a_p2, = ax.plot([], [], c='tab:red', lw=2)
# The arc of the circle for tooth N+1.
a_arc, = ax.plot([], [], c='tab:red', lw=2)
# Make sure circles are circular.
ax.axis('square')
ax.grid()
ax.set_xlim(-0.2, np.sqrt(nmax) + 0.1)
ax.set_ylim(-1., 2.)
ax.set_yticks([0, 1])
ax.set_xticks([np.sqrt(n) for n in range(nmax+1)])
ax.set_xticklabels([0, 1] + [r'$\sqrt{' + str(n) + '}$' for n in range(2, nmax+1)])
a_txt1 = ax.text(0.5, +PAD, '', ha='center', va='top', weight='bold', color='k')
a_txt2 = ax.text(0.5, -PAD, '', ha='center', va='top', weight='bold', color='tab:red')
return a_pts, a_p1, a_p2, a_arc, a_txt1, a_txt2
fig, ax = plt.subplots()
nmax = 10
def animate(N):
"""Advance the animation to sqrt(N+1) in frame N."""
cyN = N % 2
x, xp = np.sqrt(N), np.sqrt(N+1)
# Highlight the "wedge" for this number in red.
a_p1.set_data([x, 0, 0], [1 - cyN, 1 - cyN, cyN])
a_p2.set_data([xp, 0, x], [cyN, cyN, 1 - cyN])
xgrid = np.linspace(x, xp, 100)
a_arc.set_data(xgrid, cyN + (-1)**cyN * np.sqrt(xp**2 - xgrid**2))
# The circle centre swaps on each frame advance.
a_pts.set_color(['k', 'tab:red'][::(cyN or -1)])
if N:
# Don't write sqrt(0).
a_txt1.set_text(r'$\mathbf{\sqrt{' + str(N) + '}}$')
a_txt1.set_x(xp / 2)
a_txt1.set_y(1 - cyN - PAD)
a_txt2.set_text(r'$\mathbf{\sqrt{' + str(N+1) + '}}$')
a_txt2.set_x(xp / 2)
a_txt2.set_y(cyN - PAD)
return a_pts, a_p1, a_p2, a_arc, a_txt1, a_txt2
# Initialization
a_pts, a_p1, a_p2, a_arc, a_txt1, a_txt2 = init()
nframes = nmax
interval = 1000
ani = animation.FuncAnimation(fig, animate, init_func=init, frames=nframes, repeat=False,
interval=interval, blit=True)
# Write to GIF.
writer = animation.PillowWriter(fps=1,
metadata=dict(artist='Me'),
bitrate=1800)
ani.save('sharks-teeth.gif', writer=writer)
plt.show()