Plotting the decision boundary of a logistic regression model

In the notation of this previous post, a logistic regression binary classification model takes an input feature vector, $\boldsymbol{x}$ , and returns a probability, $\hat{y}$ , that $\boldsymbol{x}$ belongs to a particular class: $\hat{y} = P(y=1|\boldsymbol{x})$ . The model is trained on a set of provided example feature vectors, $\boldsymbol{x}^{(i)}$ , and their classifications, $y^{(i)} = 0$ or $$1$$ , by finding the set of parameters that minimize the difference between $\hat{y}^{(i)}$ and $y^{(i)}$ in some sense.

These model parameters are the components of a vector, $\boldsymbol{w}$ and a constant, $$b$$ , which relate a given input feature vector to the predicted logit or log-odds, $$z$$ , associated with $\boldsymbol{x}$ belonging to the class $$y=1$$ through

z = \boldsymbol{w}^T\boldsymbol{x} + b.

In this formulation,

z = \ln \frac{\hat{y}}{1-\hat{y}} \quad \Rightarrow \hat{y} = \sigma(z) = \frac{1}{1+\mathrm{e}^{-z}}.

Note that the relation between $$z$$ and the components of the feature vector, $$x_j$$ , is linear. In particular, for a two-dimensional problem,

\[z = w_1x_1 + w_2x_2 + b.\]

It is sometimes useful to be able to visualize the boundary line dividing the input space in which points are classified as belonging to the class of interest, $$y=1$$ , from that space in which points do not. This could be achieved by calculating the prediction associated with $\hat{y}$ for a mesh of $$(x_1, x_2)$$ points and plotting a contour plot (see e.g. this scikit-learn example).

Alternatively, one can think of the decision boundary as the line $$x_2 = mx_1 + c$$ , being defined by points for which $\hat{y}=0.5$ and hence $$z=0$$ . For $$x_1 = 0$$ we have $$x_2=c$$ (the intercept) and

0 = 0 + w_2x_2 + b \quad \Rightarrow c = -\frac{b}{w_2}.

For the gradient, $$m$$ , consider two distinct points on the decision boundary, $$(x_1^a,x_2^a)$$ and $$(x_1^b,x_2^b)$$ , so that $$m = (x_2^b-x_2^a)/(x_1^b-x_1^a)$$ . Along the boundary line,

\begin{align*} & 0 = w_1x_1^b + w_2x_2^b + b - (w_1x_1^a + w_2x_2^a + b)\\ \Rightarrow & -w_2(x_2^b - x_2^a) = w_1(x_1^b - x_1^a)\\ \Rightarrow & m = -\frac{w_1}{w_2}. \end{align*}

To see this in action, consider the data in linpts.txt, which maybe classified using scikit-learn's LogisticRegression classifier. The following script retrieves the decision boundary as above to generate the following visualization.

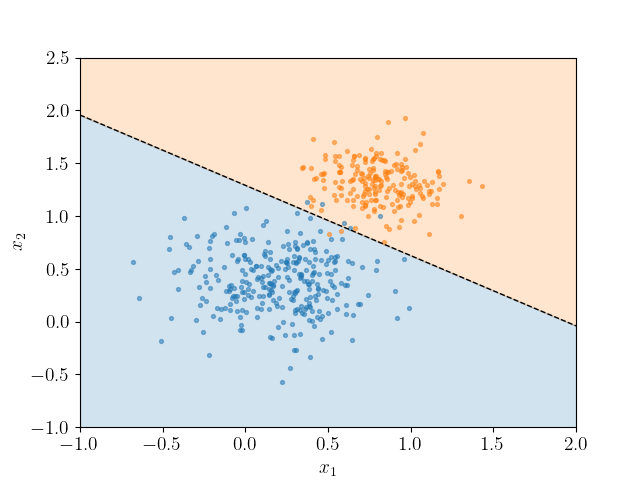
Logistic regression decision boundary

import numpy as np
import matplotlib.pyplot as plt
import sklearn.linear_model
plt.rc('text', usetex=True)

pts = np.loadtxt('linpts.txt')
X = pts[:,:2]
Y = pts[:,2].astype('int')

# Fit the data to a logistic regression model.
clf = sklearn.linear_model.LogisticRegression()
clf.fit(X, Y)

# Retrieve the model parameters.
b = clf.intercept_[0]
w1, w2 = clf.coef_.T
# Calculate the intercept and gradient of the decision boundary.
c = -b/w2
m = -w1/w2

# Plot the data and the classification with the decision boundary.
xmin, xmax = -1, 2
ymin, ymax = -1, 2.5
xd = np.array([xmin, xmax])
yd = m*xd + c
plt.plot(xd, yd, 'k', lw=1, ls='--')
plt.fill_between(xd, yd, ymin, color='tab:blue', alpha=0.2)
plt.fill_between(xd, yd, ymax, color='tab:orange', alpha=0.2)

plt.scatter(*X[Y==0].T, s=8, alpha=0.5)
plt.scatter(*X[Y==1].T, s=8, alpha=0.5)
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.ylabel(r'$x_2$')
plt.xlabel(r'$x_1$')

plt.show()