More than 3000 nuclides (atomic species characterised by the number of neutrons and protons in their nuclei) are known, most of them radioactive with a half-life of less than an hour. About 250 or so of them are stable (not observed to decay using presently-available instruments). The IAEA has an interactive online browser of the nuclides.

The script below indicates the half-lives of the nuclides listed on the Japan Atomic Energy Agency's Nuclear Data web page. The so-called valley of stability is the diagonal region along the centre of the field of plotted data. Note that the greater the number of protons in a nucleus, the more neutrons are required to stabilize it.

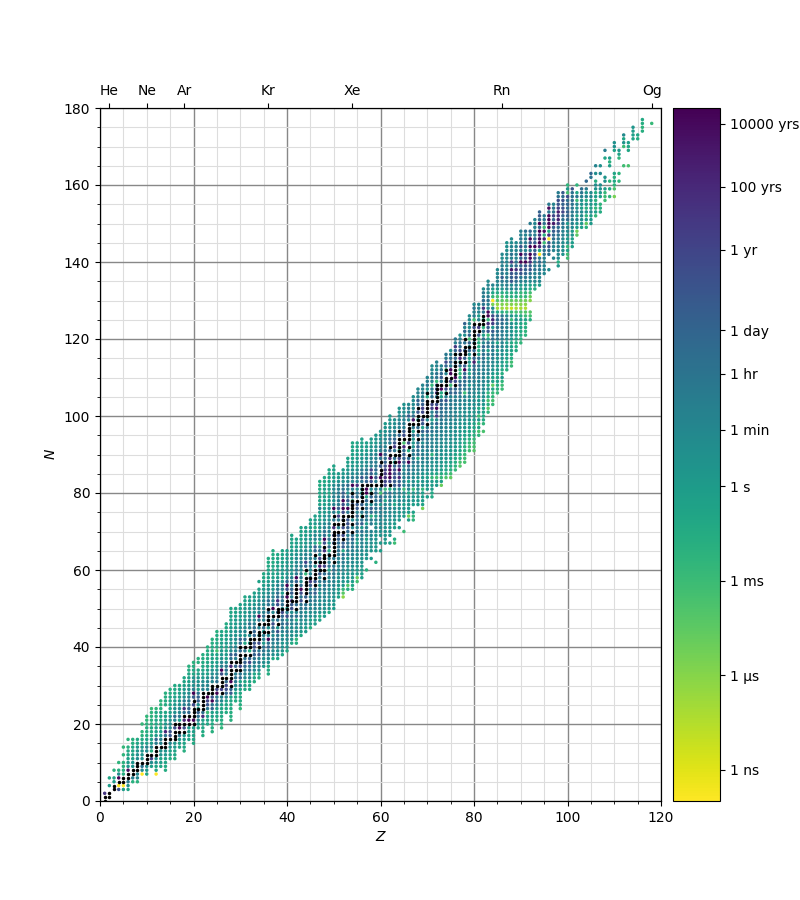
Stable nuclides are indicated in black and radioactive nuclides plotted in markers coloured on a logarithmic scale according to their half-lives. The input data file is halflives.txt.

A certain amount of work is involved in keeping the scatter plot markers at an appropriate size as the interactive Matplotlib window is resized. The function get_marker_size achieves this by obtaining the Axes dimensions, deducing the spacing between the grid points in points (1/72") and setting the size attribute (indicating the marker area in points squared) to keep the markers at a more-or-less constant proportion of the plot area.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import Normalize
from matplotlib.cm import ScalarMappable
from matplotlib import ticker
PTS_PER_INCH = 72

element_symbols = [
 'H', 'He', 'Li', 'Be',  'B',  'C',  'N',  'O',  'F', 'Ne', 'Na', 'Mg', 'Al',
'Si',  'P',  'S', 'Cl', 'Ar',  'K', 'Ca', 'Sc', 'Ti',  'V', 'Cr', 'Mn', 'Fe',
'Co', 'Ni', 'Cu', 'Zn', 'Ga', 'Ge', 'As', 'Se', 'Br', 'Kr', 'Rb', 'Sr',  'Y',
'Zr', 'Nb', 'Mo', 'Tc', 'Ru', 'Rh', 'Pd', 'Ag', 'Cd', 'In', 'Sn', 'Sb', 'Te',
 'I', 'Xe', 'Cs', 'Ba', 'La', 'Ce', 'Pr', 'Nd', 'Pm', 'Sm', 'Eu', 'Gd', 'Tb',
'Dy', 'Ho', 'Er', 'Tm', 'Yb', 'Lu', 'Hf', 'Ta',  'W', 'Re', 'Os', 'Ir', 'Pt',
'Au', 'Hg', 'Tl', 'Pb', 'Bi', 'Po', 'At', 'Rn', 'Fr', 'Ra', 'Ac', 'Th', 'Pa',
 'U', 'Np', 'Pu', 'Am', 'Cm', 'Bk', 'Cf', 'Es', 'Fm', 'Md', 'No', 'Lr', 'Rf',
'Db', 'Sg', 'Bh', 'Hs', 'Mt', 'Ds', 'Rg', 'Cn', 'Nh', 'Fl', 'Mc', 'Lv', 'Ts',
'Og'
]

def get_marker_size(ax, nx, ny):
    """Determine the appropriate marker size (in points-squared) for ax."""

    # Get Axes width and height in pixels.
    bbox = ax.get_window_extent().transformed(fig.dpi_scale_trans.inverted())
    width, height = bbox.width, bbox.height
    # Spacing between scatter point centres along the narrowest dimension.
    spacing = min(width, height) * PTS_PER_INCH / min(nx, ny)
    # Desired radius of scatter points.
    rref =  spacing / 2 * 0.5
    # Initial scatter point size (area) in pt^2.
    s = np.pi * rref**2
    return s

# Read in the data, determining the nuclide half-lives as a function of the
# number of neutrons, N, and protons, Z. Stable nuclides are indicated with
# -1 in the half-life field: deal with these separately from the radioactive
# nuclei.
halflives = {}
stables = []
for line in open('halflives.txt'):
    line = line.rstrip()
    halflife = line[10:]
    if halflife == 'None':
        continue
    fields = line[:10].split('-')
    symbol = fields[0]
    A = int(fields[1].split()[0])
    Z = int(element_symbols.index(symbol)) + 1
    N = A - Z
    halflife = float(halflife)
    if halflife < 0:
        stables.append((N, Z))
    else:
        halflives[(N, Z)] = halflife

# Unwrap the halflives dictionary into sequences of N, Z, thalf; take the log.
k, thalf = zip(*halflives.items())
N, Z = zip(*k)
maxN, maxZ = 180, 120
log_thalf = np.log10(thalf)

# Initial dimensions of the plot (pixels); figure resolution (dots-per-inch).
w, h = 800, 900
DPI = 100
w_in, h_in = w / DPI, h / DPI
# Set up the figure: one Axes object for the plot, another for the colourbar.
fig, (ax, cax) = plt.subplots(1, 2,
                        gridspec_kw={'width_ratios': [12, 1], 'wspace': 0.04},
                        figsize=(w_in, h_in), dpi=DPI)

# Pick a colourmap and set the normalization: nuclides with half-lives of less
# than 10^vmin or greater than 10^vmax secs are off-scale.
cmap = plt.get_cmap('viridis_r')
norm = Normalize(vmin=-10, vmax=12)
colours = cmap(norm(log_thalf))
s = get_marker_size(ax, maxZ, maxN)
sc1 = ax.scatter(Z, N, c=colours, s=s)
# Stable nuclides are plotted in black ('k').
Nstable, Zstable = zip(*stables)
sc2 = ax.scatter(Zstable, Nstable, c='k', s=s, label='stable')

# Jump through the usual hoops to get a grid on both major and minor ticks
# under the data.
loc = ticker.MultipleLocator(base=5)
ax.xaxis.set_minor_locator(loc)
ax.yaxis.set_minor_locator(loc)
ax.grid(which='minor', color='#dddddd')
ax.grid(which='major', color='#888888', lw=1)
ax.set_axisbelow(True)

ax.set_xlim(0, maxZ)
ax.set_ylim(0, maxN)
ax.set_xlabel(r'$Z$')
ax.set_ylabel(r'$N$')

# Twin the y-axis to indicate the noble gas elements on the top x-axis.
topax = ax.twiny()
topax.set_xticks([2, 10, 18, 36, 54, 86, 118])
topax.set_xticklabels(['He', 'Ne', 'Ar', 'Kr', 'Xe', 'Rn', 'Og'])
topax.set_xlim(0, maxZ)

# The colourbar: label key times in appropriate units.
cbar = fig.colorbar(ScalarMappable(norm=norm, cmap=cmap), cax=cax)
SECS_PER_DAY = 24 * 3600
SECS_PER_YEAR = 365.2425 * SECS_PER_DAY
cbar_ticks = np.log10([1.e-9, 1.e-6, 1.e-3, 1, 60, 3600, SECS_PER_DAY,
                   SECS_PER_YEAR, 100 * SECS_PER_YEAR, 10000 * SECS_PER_YEAR])
cbar_ticklabels = ['1 ns', '1 μs', '1 ms', '1 s', '1 min', '1 hr', '1 day',
                   '1 yr', '100 yrs', '10000 yrs']
cbar.set_ticks(cbar_ticks)
cbar.set_ticklabels(cbar_ticklabels)

def on_resize(event):
    """Callback function on interactive plot window resize."""
    # Resize the scatter plot markers to keep the plot looking good.
    s = get_marker_size(ax, maxZ, maxN)
    sc1.set_sizes([s]*len(Z))
    sc2.set_sizes([s]*len(stables))

# Attach the callback function to the window resize event.
cid = fig.canvas.mpl_connect('resize_event', on_resize)

plt.savefig('nuclide-halflifes.png', dpi=DPI)
plt.show()