The binding energy of a nucleus is the energy that would be required to split apart each of its constituent protons and neutrons (nucleons). This energy is due to the forces that hold the nucleus together, which may be thought of as a balance between the attractive strong nuclear force and the electromagnetic force (which is repulsive between the positively-charged protons). The binding energy manifests itself in a mass difference between the nucleus and the individual nucleons ($E=mc^2$) and the difference in binding energy between different nuclei is the energy released in the process of nuclear fusion and fission.

The OECD's Nuclear Energy Agency publishes a compilation of nuclear data including recommended values for binding energies: mass.mas03 (G. Audi, A. H. Wapstra and C. Thibault, "The Ame2003 atomic mass evaluation (II)", Nuclear Physics A729, 337–676 (2003).) The binding energy reported is an average per nucleon: $\bar{E}_\mathrm{bind} = E_\mathrm{bind} / A$ where $A=N+Z$ is the total number of nucleons, the sum of the number of neutrons, $N$ and protons, $Z$.

A semi-emprical mass formula (SEMF) based on the George Gamow's so-called liquid drop model can be used to estimate mean binding energies:

$$ \bar{E}_\mathrm{bind} = a_V - a_S A^{-1/3} - a_C Z^2 A^{-4/3} - a_A (A-2Z)^2A^{-2} \pm \delta A^{-3/2} $$

A brief description of these parameters is given below; more details can be found in standard textbooks on nuclear physics, and in outline on Wikipedia. Parameter values are taken from J. W. Rohlf, Modern Physics from $\alpha$ to $Z^0$, Wiley (1994).

Parameter	Value /MeV	Description
$a_V$	15.75	Volume term, due to the strong nuclear force
$a_S$	17.8	Surface term, a correction to the volume term due to reduced interactions with nucleons at the surface of the nucleus
$a_C$	0.711	Coulomb term, due to electrostatic repulsions between the protons
$a_A$	23.7	Asymmetry term, explained by the need for nucleons to obey the Fermi exclusion principle
$\pm \delta$	$\pm 11.18$, $0$	Pairing term, accounting for the effects of spin coupling. The positive sign applies to nuclei with $Z$ and $N$ both even; the negative sign to nuclei with $Z$ and $N$ both odd; otherwise this term is zero

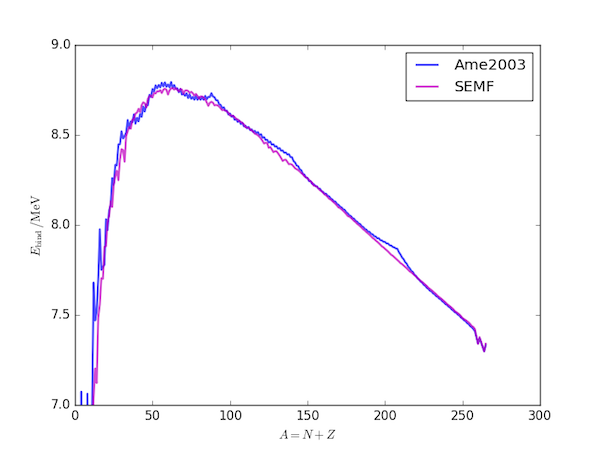
The following code generates the above plot of the recommended NEA binding energies and those derived using the SEMF approximation.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def SEMF(Z, N):
    """Calculate the average binding energy per nucleon for nucleus Z, N.

    Calculate the average nuclear binding energy per nucleon for a nucleus
    with Z protons and N neutrons, using the semi-empirical mass formula and
    parameters of J. W. Rohlf, "Modern Physics from alpha to Z0", Wiley (1994).

    Z and N can be NumPy arrays or scalar values.

    """

    # The parameterization of the SEMF to use.
    aV, aS, aC, aA, delta = 15.75, 17.8, 0.711, 23.7, 11.18

    # Covert Z and N to NumPy arrays if they aren't already
    Z, N = np.atleast_1d(Z), np.atleast_1d(N)
    # Total number of nucleons
    A = Z + N

    # The pairing term is -delta for Z and N both odd, +delta for Z and N both
    # even, and 0 otherwise. Create an array of the sign of this term so that
    # we can vectorize the calculation across the arrays Z and N.
    sgn = np.zeros(Z.shape)
    sgn[(Z%2) & (N%2)] = -1
    sgn[~(Z%2) & ~(N%2)] = +1

    # The SEMF for the average binding energy per nucleon.
    E = (aV - aS / A**(1/3) - aC * Z**2 / A**(4/3) -
         aA * (A-2*Z)**2/A**2 + sgn * delta/A**(3/2))

    # Return E as a scalar or array as appropriate to the input Z.
    if Z.shape[0] == 1:
        return float(E)
    return E

# Read the experimental data into a Pandas DataFrame.
df = pd.read_fwf('mass.mas03', usecols=(2,3,4,11),
              widths=(1,3,5,5,5,1,3,4,1,13,11,11,9,1,2,11,9,1,3,1,12,11,1),
              skiprows=39, header=None,
              index_col=False)
df.columns = ('N', 'Z', 'A', 'avEbind')

# Extrapolated values are indicated by '#' in place of the decimal place, so
# the avEbind column won't be numeric. Coerce to float and drop these entries.
df['avEbind'] = pd.to_numeric(df['avEbind'], errors='coerce')
df = df.dropna()
# Also convert from keV to MeV.
df['avEbind'] /= 1000

# Group the DataFrame by nucleon number, A.
gdf = df.groupby('A')
# Find the rows of the grouped DataFrame with the maximum binding energy.
maxavEbind = gdf.apply(lambda t: t[t.avEbind==t.avEbind.max()])

# Add a column of estimated binding energies calculated using the SEMF.
maxavEbind['Eapprox'] = SEMF(maxavEbind['Z'], maxavEbind['N'])

# Generate a plot comparing the experimental with the SEMF values.
fig, ax = plt.subplots()
ax.plot(maxavEbind['A'], maxavEbind['avEbind'], alpha=0.7, lw=2,
            label='Ame2003')
ax.plot(maxavEbind['A'], maxavEbind['Eapprox'], alpha=0.7, lw=2, c='m',
            label='SEMF')
ax.set_xlabel(r'$A = N + Z$')
ax.set_ylabel(r'$E_\mathrm{bind}\,/\mathrm{MeV}$')
ax.legend()
# We don't expect the SEMF to work very well for light nuclei with small
# average binding energies, so display only data relevant to avEbind > 7 MeV.
ax.set_ylim(7,9)
plt.show()