Iceberg dynamics
Posted on 22 February 2021
Prompted by this tweet and campaign for icebergs to be depicted in their most stable equilibrium orientation, here is a Python script modelling the dynamics of a two-dimensional iceberg which starts in an arbitrary orientation and position and relaxes under gravitational and buoyant forces to its most stable configuration. A cork floats "on its side": with its longest axis parallel to the water's surface (it doesn't bob around with its longest axis vertical), and an iceberg does the same.
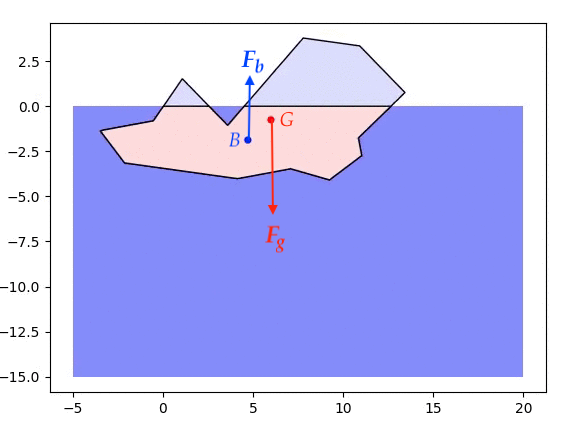
The centre of mass ($G$) and the centre of buoyancy ($B$, the centre of mass of the displaced water) are indicated by the red and blue dots respectively. The motion of the iceberg (treated as a rigid body) is dictated by the force of gravity ($\boldsymbol{F}_g$) and an opposing buoyant force ($\boldsymbol{F}_b$) due to the displaced water. In addition to any translational force moving the centre of mass of the iceberg, where these forces are not colinear they exert a torque, $\boldsymbol{\tau} = \boldsymbol{r} \times \boldsymbol{F}_b$, where $r$ is the vector from $G$ to $B$, which tends to rotate the iceberg.
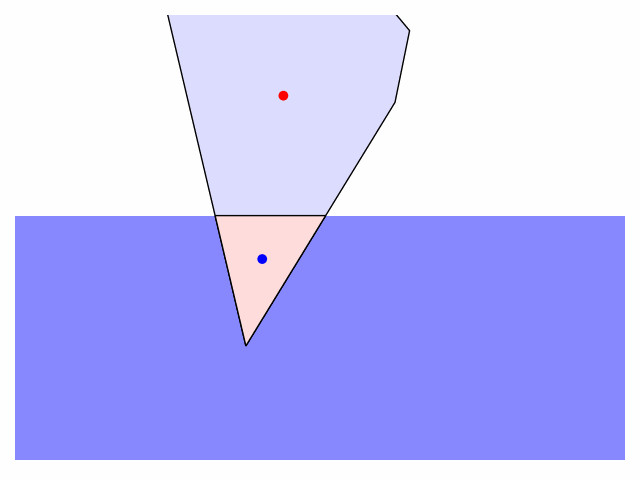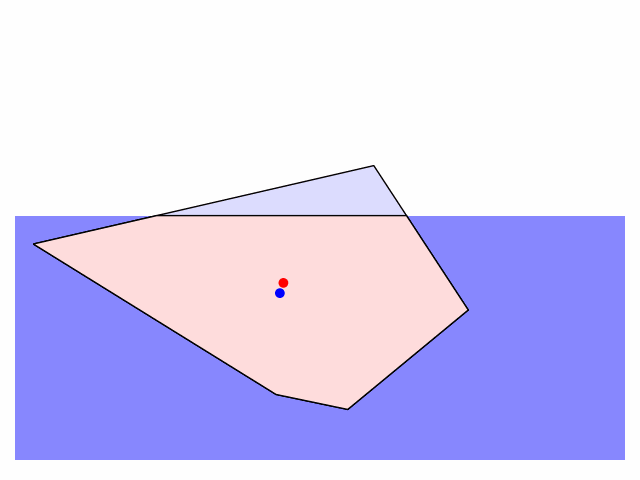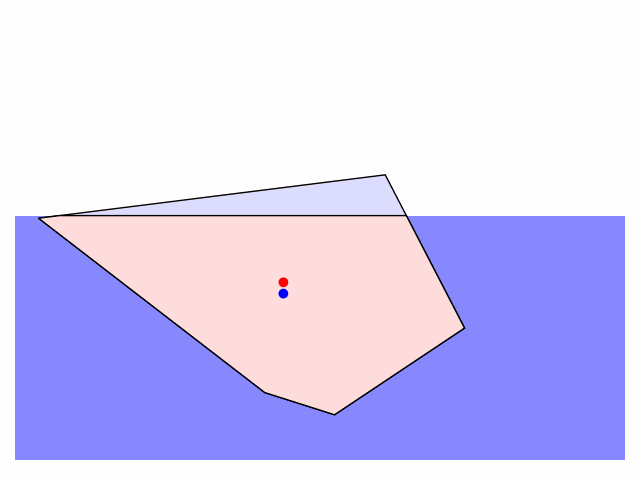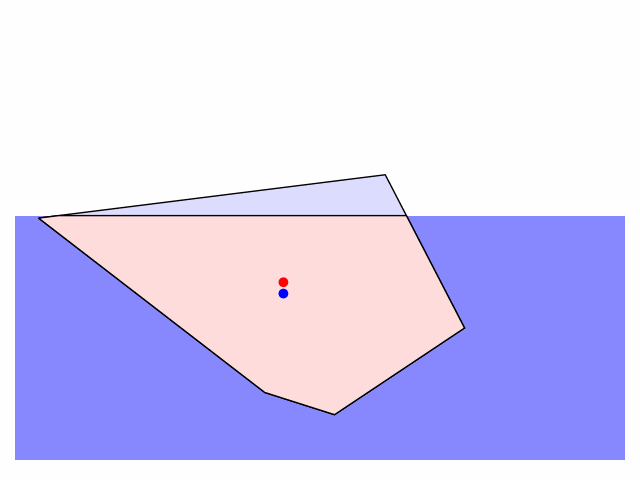
There are few things one can customize in the code: the shape of the iceberg (defined as a sequence of vertex coordinates), the initial position ($h$) and orientation (call rotate_poly to rotate the iceberg to a given angle), and the friction applied to damp the rotation and translation of the iceberg in water (edit the apply_friction function). I'll tidy up and post the code on GitHub when I get a moment.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animation
# Plot limits: ideally the figure will not have to rescale during the animation
xmin, xmax = -5, 20
ymin, ymax = -10, 8
width, height = xmax - xmin, ymax - ymin
# The area density of sea water and ice.
rho_water, rho_ice = 1.027, 0.9
# Acceleration due to gravity, m.s-2
g = 9.81
def canonicalize_poly(xy):
"""Shift the (N+1,2) array of coordinates xy to start at minimum y."""
#if get_area(xy) > 0:
# xy = xy[::-1]
idx_ymin = xy[:,1].argmin()
xy = np.roll(xy[:-1], -idx_ymin, axis=0)
return np.vstack((xy, xy[0]))
def rotate_poly(xy, theta):
"""Rotate the (N+1,2) array of coordinates xy by angle theta about (0,0).
The rotation angle, theta, is in radians.
"""
s, c = np.sin(theta), np.cos(theta)
R = np.array(((c, -s), (s, c)))
xyp = (R @ xy.T).T
return canonicalize_poly(xyp)
def get_area(xy):
"""Return the area of the polygon xy.
xy is a (N+1,0) NumPy array defining the N polygon vertices, but repeating
the first vertex as its last element. The "shoelace algorithm" is used.
"""
x, y = xy.T
return np.sum(x[:-1]*y[1:] - x[1:]*y[:-1]) / 2
def get_cofm(xy, A=None):
"""Return the centre of mass of the polygon xy.
xy is a (N+1,0) NumPy array defining the N polygon vertices, but repeating
the first vertex as its last element. If the polygon area is not passed
in as A it is calculated. The polygon must have uniform density.
"""
if A is None:
A = get_area(xy)
x, y = xy.T
Cx = np.sum((x[:-1] + x[1:]) * (x[:-1]*y[1:] - x[1:]*y[:-1])) / 6 / A
Cy = np.sum((y[:-1] + y[1:]) * (x[:-1]*y[1:] - x[1:]*y[:-1])) / 6 / A
return np.array((Cx, Cy))
def get_moi(xy, rho):
"""Return the moment of inertia of the polygon xy with density rho.
xy is a (N+1,0) NumPy array defining the N polygon vertices, but repeating
the first vertex as its last element.
"""
x, y = xy.T
Ix = rho * np.abs(np.sum((x[:-1]*y[1:] - x[1:]*y[:-1]) *
(y[:-1]**2 + y[:-1]*y[1:] + y[1:]**2)) / 12)
Iy = rho * np.abs(np.sum((x[:-1]*y[1:] - x[1:]*y[:-1]) *
(x[:-1]**2 + x[:-1]*x[1:] + x[1:]**2)) / 12)
# Perpendicular axis theorem.
Iz = Ix + Iy
return Ix, Iy, Iz
def get_zero_crossing(pts):
"""Return the coordinates of the zero-crossing in pts.
pts is a pair of (x, y) points, assumed to be joined by a straight line
segment. This function returns the coordinates (x,0) at which this line
crosses the y-axis (corresponding to sea-level in our model).
"""
P0, P1 = pts
x0, y0 = P0
x1, y1 = P1
if (x1-x0) == 0:
return x1, 0
m = (y1-y0)/(x1-x0)
c = y1 - m*x1
return -c/m, 0
def get_displaced_water_poly(iceberg, submerged=None):
"""Get the polygon for the submerged portion of the iceberg.
iceberg is a (N+1,2) array of coordinates corresponding to the iceberg's
vertexes in its current position and orientation (the first vertex is
repeated at the end of the array);
submerged is a boolean array corresponding to the vertexes which are
under water (<0); if not provided it is calculated.
"""
if submerged is None:
submerged = (iceberg[:,1] <= 0)
nsubmerged = sum(submerged)
# Partially-submerged iceberg: find where it enters the sea, i.e. which
# edges cross zero. zc_idx holds the indexes of the vertices *before*
# each zero-crossing edge.
diff = np.diff(submerged)
zc_idx = np.where(diff)[0]
# Interpolate to find the coordinates of the zero crossing.
ncrossings = len(zc_idx)
# We're going to build a polygon for the shape of the displaced water,
# i.e. the submerged part of the iceberg.
displaced_water = np.empty((nsubmerged + ncrossings, 2))
# Loop over the points *before* each crossing in pairs. NB if the
# iceberg is partially submerged, len(zc_idx) is guaranteed to be even.
assert not ncrossings % 2
i = j = 0
for idx1, idx2 in zip(zc_idx[0::2], zc_idx[1::2]):
# All the submerged vertices up to the upwards crossing.
displaced_water[j:j+idx1-i+1] = iceberg[i:idx1+1]
# Work out where the crossing vertex should be and add it.
c = get_zero_crossing(iceberg[idx1:idx1+2])
j += idx1 - i + 1
displaced_water[j] = c
j += 1
# Now the downward crossing: all the unsubmerged vertices are
# skipped, and an extra vertex at sea level is added.
c = get_zero_crossing(iceberg[idx2:idx2+2])
displaced_water[j] = c
j += 1
i = idx2 + 1
# Copy across any remaining submerged vertexes to displaced_water.
displaced_water[j:] = iceberg[i:]
return displaced_water
def apply_friction(omega, dh):
"""Apply frictional forces to the angular and linear velocities."""
# Hard friction: angular and linear velocities are immediately quenched.
# after movement.
# return 0, np.array((0,0))
# Intermediate friction: reduce the velocities by some fraction.
return omega * 0.95, dh * 0.65
# Our two-dimensional iceberg, defined as a polygon.
poly = [(0,0), (5, -4), (5, -7), (1, -18), (-5, -5)]
# Repeat the initial vertex at the end, for convenience.
iceberg0 = np.array(poly + [poly[0]])
# Centre the iceberg's local coordinates on its centre of mass.
iceberg0 = iceberg0 - get_cofm(iceberg0)
# We might want to start the iceberg off in some different orientation:
# if so, rotate it here.
iceberg0 = rotate_poly(iceberg0, -0.2)
# Get the (signed) area, mass, and weight of the iceberg.
A = get_area(iceberg0)
M = rho_ice * abs(A)
Fg = np.array((0, -M * g))
# We also need the Iz component of the iceberg's moment of inertia.
_, _, Iz = get_moi(iceberg0, rho_ice)
fig, ax = plt.subplots()
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
# We would prefer equal distances in the x- and y-directions to look the same.
ax.axis('equal')
ax.axis('off')
fig.tight_layout()
# The centre of mass starts at this height above sea level.
h = 5
# theta is the turning angle of the iceberg from its initial orientation;
# G is the position of its centre of mass (in world coordinates).
theta, G = 0, np.array((6, h))
# omega = dtheta / dt is the angular velocity; dh is the linear velocity.
omega, dh = 0, np.array((0,0))
# The time step (s): small, but not too small.
dt = 0.1
def update(it):
"""Update the animation for iteration number it."""
global omega, dh, G, theta
print('iteration #{}'.format(it))
# Update iceberg orientation and position.
theta += omega * dt
G = G + dh * dt
# Rotate and translate a copy of the original iceberg into its current.
# position.
iceberg = rotate_poly(iceberg0, theta)
iceberg = iceberg + G
# Which vertices are submerged (have their y-coordinate negative)?
submerged = (iceberg[:,1] <= 0)
nsubmerged = sum(submerged)
iceberg_in_water = True
if nsubmerged in (0, 1):
# The iceberg is in the air above the surface of the sea.
B = None
Adisplaced = 0
alpha = 0
iceberg_in_water = False
if iceberg_in_water:
# Apply some frictional forces which damp the motion in water.
omega, dh = apply_friction(omega, dh)
if nsubmerged == len(submerged):
# The iceberg is fully submerged.
displaced_water = iceberg
Adisplaced = A
B = G
else:
displaced_water = get_displaced_water_poly(iceberg, submerged)
# Area of the displaced water and position of the centre of buoyancy.
Adisplaced = get_area(displaced_water)
B = get_cofm(displaced_water)
# Buoyant force due to the displaced water.
Fb = np.array((0, rho_water * abs(Adisplaced) * g))
if B is not None:
# Vector from G to B
r = B - G
# Torque about G
tau = np.cross(r, Fb)
alpha = tau / Iz
# Resultant force on the iceberg.
F = Fg + Fb
# Net linear acceleration.
a = F / M
# Now plot the scene for this frame of the animation.
ax.clear()
# The sea! The sea!
sea_patch = plt.Rectangle((xmin, ymin), width, -ymin, fc='#8888ff')
ax.add_patch(sea_patch)
# The iceberg itself, in its current orientation and position.
poly_patch = plt.Polygon(iceberg, fc='#ddddff', ec='k')
ax.add_patch(poly_patch)
if B is not None:
# Draw the submerged part of the iceberg in a different colour.
poly_patch = plt.Polygon(displaced_water, fc='#ffdddd', ec='k')
ax.add_patch(poly_patch)
# Indicate the position of the centre of buoyancy.
bofm_patch = plt.Circle(B, 0.2, fc='b')
ax.add_patch(bofm_patch)
# Indicate the position of the centre of mass.
cofm_patch = plt.Circle(G, 0.2, fc='r')
ax.add_patch(cofm_patch)
# Update the angular and linear velocities
omega += alpha * dt
dh = dh + a * dt
ax.set_xlim(xmin, xmax)
ax.set_ylim(ymin, ymax)
ax.axis('off')
ani = animation.FuncAnimation(fig, update, 300, blit=False, interval=100, repeat=True)
plt.show()