The temperature-dependence of the rotational contribution to the heat capacity of gaseous molecular hydrogen shows a Schottky anomaly: whereas for many systems the heat capacity can be expected to increase with increasing temperature, for $\mathrm{H_2}$ there is an temperature range within which it reaches a maximum before decreasing. Only at higher temperatures does it revert to "conventional" behaviour.

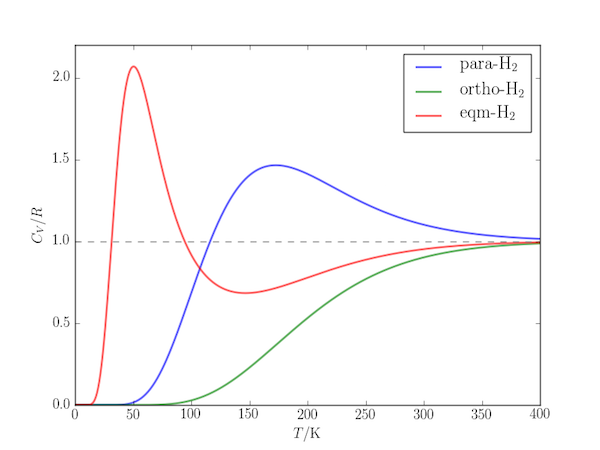
The Schottky anomaly in this case can be explained by the unusually large rotational constant of the molecule: ($B = 60.9\;\mathrm{cm^{-1}}$). Below 200 K it can behave like a two-level system with only the two lowest rotational levels thermally accessible and the next highest "out of reach". The effect is enhanced by nuclear spin statistics:

• For ortho-$\mathrm{H_2}$ only odd-$J$ levels exist (the lowest lying are 1 and 3, separated by $\Delta E = 10B$). Where the temperature is such that the second is thermally accessible, the next highest ($J=5$ a further $18B$ higher in energy) also contributes and no Schottky anomaly is seen.
• For para-$\mathrm{H_2}$ only even-$J$ levels exist. There is a relatively large gap between the first two ($E_0 = 0$ and $E_2 = 6B$) and the next highest ($E_4 = 20B$) and a pronounced peak in the temperature range where only these lowest levels contribute.
• In the presence of a metal catalyst to maintain equilibrium between ortho- and para-$\mathrm{H_2}$ there is additional contribution from the nuclear spin degeneracy: there is three times as much of the triplet ortho-$\mathrm{H_2}$. The lowest three levels are then $E_0 = 0$, $E_1 = 2B$ and $E_2 = 6B$ with degeneracies $g_0 = 1$, $g_1 = 3\times 3 = 9$, $g_2 = 5$, and a very pronounced peak at low temperature, dominated by the two-level effect of $E_0$ and $E_1$.

The effect is obvious if the heat capacity for the corresponding two-level systems is plotted alongside the molecular heat capacity:

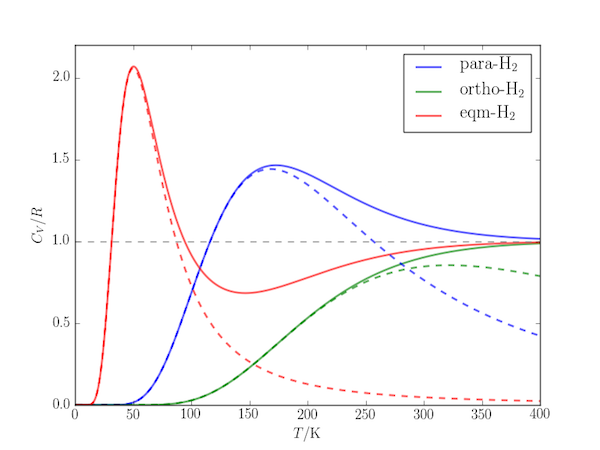
The following code uses the partition_function.py module of the previous post to calculate the molar heat capacity at constant volume, $C_{V,\mathrm{m}}$ at temperatures up to 400 K for each of the above cases.

import numpy as np
from scipy.constants import k as kB, R
import matplotlib.pyplot as plt
from matplotlib import rc

from partition_function import calc_CV

rc('font', **{'family': 'serif', 'serif': ['Computer Modern'], 'size': 14})
rc('text', usetex=True)
GREY = (0.5, 0.5, 0.5)

# Rotational constant, temperature grid (K).
B = 60.9
T = np.linspace(1,400,401)
beta = 1/kB/T

def gns_H2_eqm(J, *args):
    """Degeneracies of equilibrium ortho-/para-H2 rotational levels."""
    if J % 2:
        # ortho-H2
        return 3
    # para-H2
    return 1

def gns_H2_ortho(J, *args):
    """Degeneracies of ortho-H2 rotational levels."""
    if J % 2:
        return 3
    return 0

def gns_H2_para(J, *args):
    """Degeneracies of para-H2 rotational levels."""
    if J % 2:
        return 0
    return 1

def Erot(J, B):
    """Rigid rotor energy levels in terms of quantum number J."""
    return B*J*(J+1)

# Dictionary of named degeneracy and energy functions.
funcs = {
    r'eqm-H$_2$': (lambda J, B: gns_H2_eqm(J) * (2*J+1), Erot),
    r'ortho-H$_2$': (lambda J, B: gns_H2_ortho(J) * (2*J+1), Erot),
    r'para-H$_2$': (lambda J, B: gns_H2_para(J) * (2*J+1), Erot)
}

# Calculate the heat capacities for the named cases.
CVs = {}
for name, (gfunc, Efunc) in funcs.items():
    CVs[name] = calc_CV(T, gfunc, Efunc, args=(B,))

# Plot the heat capacities against temperature
for name in (r'para-H$_2$', r'ortho-H$_2$', r'eqm-H$_2$'):
    plt.plot(T, CVs[name]/R, label=name, lw=2, alpha=0.6)
plt.legend(loc=1)
plt.xlabel(r'$T/\mathrm{K}$')
plt.ylabel(r'$C_V/R$')
plt.ylim(0,2.2)
plt.axhline(1, ls='--', c=GREY)
plt.savefig('H2-CV.png')
plt.show()

# Two-level systems: degeneracy and energy level functions
def E_2level_para(i, B):
    """para-H2 energies: the lowest two states are J=0 and J=2."""
    if i == 0: return 0
    if i == 1: return 6 * B
    return None
def g_2level_para(i, *args):
    """para-H2 degeneracies: the lowest two states are J=0 and J=2."""
    return 5 if i else 1

def E_2level_ortho(i, B):
    """ortho-H2 energies: the lowest two states are J=1 and J=3."""
    if i == 0: return 0
    if i == 1: return 10 * B
    return None
def g_2level_ortho(i, *args):
    """ortho-H2 degeneracies: the lowest two states are J=1 and J=3."""
    return 21 if i else 9

def E_2level_eqm(J, B):
    """Equilibrium-H2 energies: the lowest states are J=0 and J=1."""
    if J == 0: return 0
    if J == 1: return 2 * B
    return None
def g_2level_eqm(J, *args):
    """Equilibrium-H2 degeneracies: the lowest states are J=0 and J=1."""
    # NB odd-J has an extra factor of 3 from the nuclear spin degeneracy.
    return 9 if J else 1

# Calculate the two-level heat capacities as a function of temperature.
CVs['2-level (para)'] = calc_CV(T, g_2level_para, E_2level_para, args=(B,))
CVs['2-level (ortho)'] = calc_CV(T, g_2level_ortho, E_2level_ortho, args=(B,))
CVs['2-level (eqm)'] = calc_CV(T, g_2level_eqm, E_2level_eqm, args=(B,))

# Plot the heat capacities against temperature
for name in (r'para-H$_2$', r'ortho-H$_2$', r'eqm-H$_2$'):
    plt.plot(T, CVs[name]/R, label=name, lw=2, alpha=0.6)
plt.plot(T, CVs['2-level (para)']/R, lw=2, alpha=0.6, c='b', ls='--')
plt.plot(T, CVs['2-level (ortho)']/R, lw=2, alpha=0.6, c='g', ls='--')
plt.plot(T, CVs['2-level (eqm)']/R, lw=2, alpha=0.6, c='r', ls='--')

plt.legend(loc=1)
plt.xlabel(r'$T/\mathrm{K}$')
plt.ylabel(r'$C_V/R$')
plt.ylim(0,2.2)
plt.axhline(1, ls='--', c=GREY)
plt.savefig('H2-CV-2level.png')
plt.show()