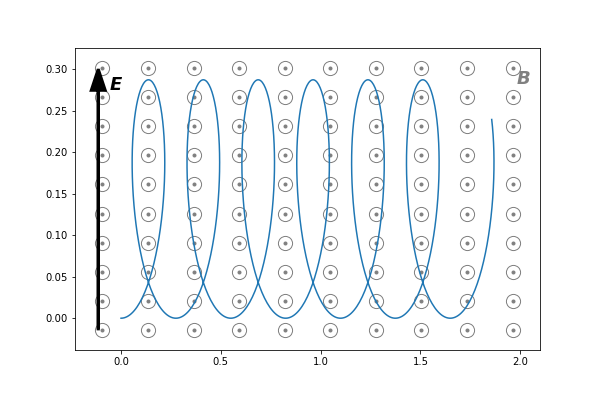
ExB drift for constant crossed electric and magnetic fields

Posted by: christian on 17 Dec 2018

(3 comments)

A charged particle moving in an electromagnetic field exhibits a "drift" in addition to its gyromotion and any acceleration due to a component of the electric field parallel to the magnetic field. This drift motion has velocity $(\boldsymbol{E}\times\boldsymbol{B})/B^2$ and is therefore known as the $\boldsymbol{E}\times\boldsymbol{B}$ drift. In the simple case of constant, crossed magnetic and electric fields, the Lorentz equation of motion, $m\ddot{\boldsymbol{r}} = q(\boldsymbol{E} + \dot{\boldsymbol{r}} \times \boldsymbol{B})$ can be solved analytically to give the particle's trajectory: $$ \begin{align} x &= \frac{1}{\Omega}\left( v_\perp - \frac{E_y}{B_z}\right)\sin \Omega t + \frac{E_y}{B_z}t,\\ y &= \frac{1}{\Omega}\left( v_\perp - \frac{E_y}{B_z}\right)\left(1 - \cos \Omega t \right),\\ z &= 0, \end{align} $$ where the fields are $\boldsymbol{B} = (0,0,B_z)$ and $\boldsymbol{E} = (0,E_y,0)$; the initial velocity is $\boldsymbol{v} = (0,v_\perp,0)$; the gyrofrequency is $\Omega = qB_z/m$; and $m$ and $q$ are the particle's mass and charge respectively.

The Jupyter Notebook here depicts this solution and is also available on my github page.

enter image description here

Current rating: 2.9

Comments

Comments are pre-moderated. Please be patient and your comment will appear soon.

Martin 2 years, 6 months ago

Hi,
there is some mistake with units for x eq. (some Omega missing or bracket missing ?)

Link | Reply
Current rating: 5

Martin 2 years, 6 months ago

Hi,
or t ?

Link | Reply
Currently unrated

christian 2 years, 6 months ago

That's it – a missing t. Thank you for the correction.
Cheers, Christian

Link | Reply
Currently unrated

New Comment

required

required (not published)

optional

required