Posted by: christian on 28 Oct 2017
This post is based on Problem 2.22 from Griffiths, Introduction to Quantum Mechanics (Prentice Hall, 1995).
A free particle prepared in the initial state $$ \Psi(x, t=0) = \sqrt{\frac{\pi}{a}} e^{-ax^2} $$ (where $a$ is a constant) evolves according to the Schrödinger equation as $$ \Psi(x,t) = \left( \frac{2a}{\pi} \right)^{1/4} \frac{e^{-ax^2/[1+(2i\hbar at/m]}}{\sqrt{1+(2i\hbar at/m)}}. $$
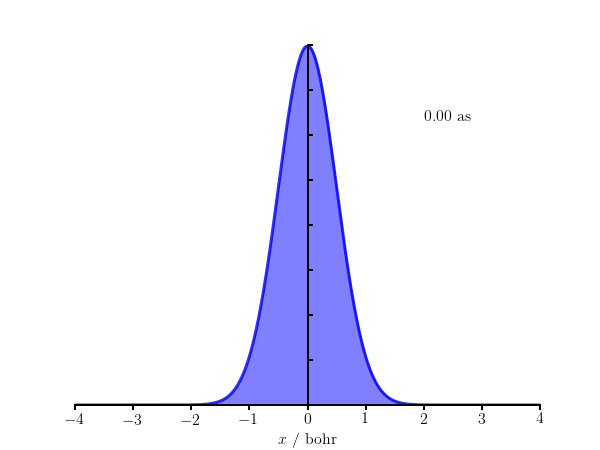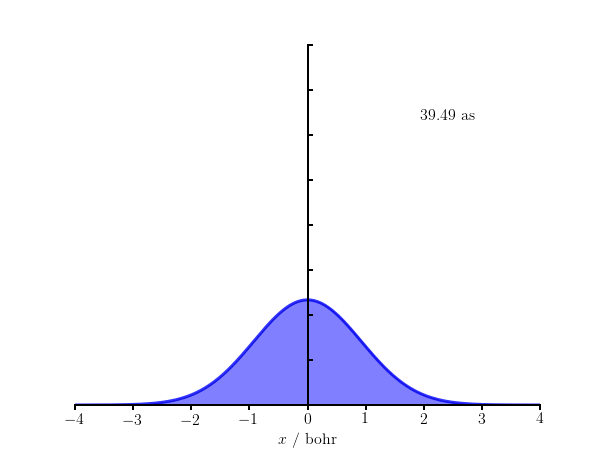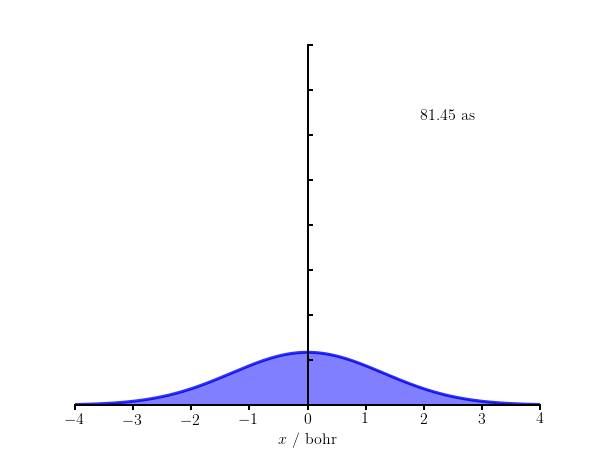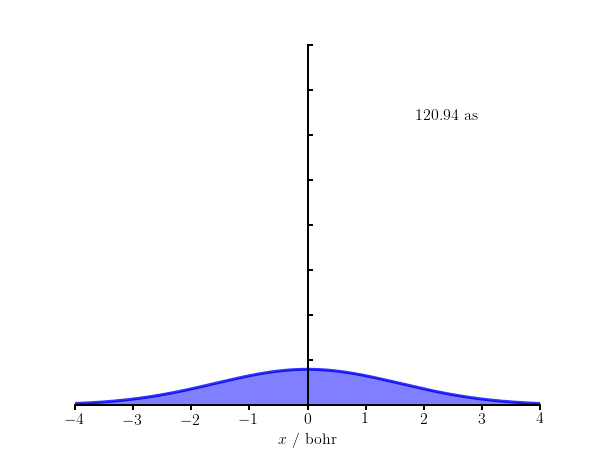
From $\Psi(x,t)$, the probability distribution function can be shown to be $$ |\Psi(x,t)|^2 = \sqrt{\frac{2a}{\pi}}\frac{e^{-2ax^2/[1+\beta^2]}}{\sqrt{1+\beta^2}}, $$ where $\beta = 2\hbar at/m$.
The code below generates the frames in the above animation of $|\Psi(x,t)|^2$ for an electron with $a = 1\;\mathrm{bohr}^{-1/2}$. We work in atomic units so $m_e = 1$ and $\hbar = 1$, but convert the time to attoseconds (as) for the annotation.
import numpy as np
from matplotlib import rc
import matplotlib.pyplot as plt
# Use LaTeX throughout the figure for consistency
rc('font', **{'family': 'serif', 'serif': ['Computer Modern'], 'size': 16})
rc('text', usetex=True)
# Position, in bohr
x = np.linspace(-4, 4, 1000)
# The constant a, in bohr^-0.5
a = 1
# hbar and hartree in SI units for the time conversion
hbar, Eh = 1.054571726e-34, 4.35974417e-18
# Grid of times (atomic units)
tgrid = np.linspace(0, 5, 50)
def plot_psi2(ax, i, t, psi2):
# Plot |psi|^2 on Axes ax for frame i, time t
ax.plot(x, psi2, c='b', lw=3, alpha=0.8)
# Fill under the line with reduced opacity
ax.fill_between(x, psi2, facecolor='b', alpha=0.5)
# Customise and tidy up the Axes
ax.set_ylim(0, 0.8)
ax.yaxis.set_tick_params(width=2, length=5)
ax.spines['left'].set_position('center')
ax.spines['left'].set_linewidth(2)
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.yaxis.set_ticks_position('left')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_linewidth(2)
ax.xaxis.set_tick_params(width=2, length=5, direction='out')
ax.yaxis.set_ticklabels([])
# Add x-axis label and annotate with time in attoseconds
t_in_as = t * hbar/Eh * 1.e18
ax.annotate(s='{:.2f} as'.format(t_in_as), xy=(0.8, 0.8),
xycoords='axes fraction', ha='center', va='center')
ax.set_xlabel('$x$ / bohr')
# Create the animation frames at 72 dpi, 600x450 pixels as PNG images
dpi = 72
for i, t in enumerate(tgrid):
w = np.sqrt(a/(1+(2*a*t)**2))
psi2 = np.sqrt(2/np.pi) * w * np.exp(-2*w*x**2)
fig = plt.figure(figsize=(600/dpi, 450/dpi), dpi=dpi)
ax = fig.add_subplot(111)
plot_psi2(ax, i, t, psi2)
plt.savefig('frames/psi2-{:02d}.png'.format(i), dpi=dpi)
plt.close()
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
There are currently no comments
New Comment