An article by Oliver and Soundararajan that has got a lot of attention in the last few days notes that there is a curious pattern in the distribution of the final digits of consecutive prime numbers. Prime numbers larger than 5 must end in 1, 3, 7 or 9 (else they would be divisible by either 2 or 5), and it seems that a prime ending in any of these is less likely to be followed by another prime ending in the same digit.

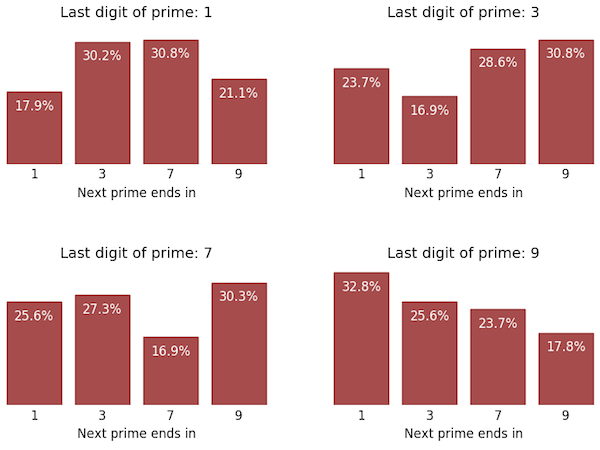
For example, in the first billion primes the authors find that a prime with final digit 1 is followed by one with final digit 1 about 18% of the time, but followed by a prime ending in 3, 7 and 9 with probabilities 30%, 30% and 22%.

Here I will verify this for the first 10 million primes (I don't have the patience to calculate a billion or the bandwidth to download them from some online service). The code below uses a segmented sieve of Eratosthenes to build a dictionary of dictionaries, mapping the last digit of each prime to the last digit of the following prime, to a count of the number of times that pair of last digits is encountered. Thus, digit_count[1][3] is the number of times a prime number ending in 1 is followed by one ending in 3.

The segmented sieve works by first generating a list of prime numbers up to the square root of a number estimated to be close to but guaranteed to be larger than the 10,000,000th prime number. The 10,000,000th prime is 179,424,673, so we only need to store the square root of this number of potential prime factors, or 13,395 of them, in a fairly modestly-sized list. This list is then used to sieve all numbers starting at 7 (the first one of interest to us for this exercise) until 10,000,000 prime numbers have been found.

The code for this project is also available on my GitHub page.

import time
import math

def approx_nth_prime(n):
    """Return an upper bound for the value of the nth prime"""

    return n * (math.log(n) + math.log(math.log(n)))

nmax = 10000000
pmax = approx_nth_prime(nmax)
print('The {:d}th prime is approximately {:d}'.format(nmax,int(pmax)))
N = int(math.sqrt(pmax)) + 1
print('Our sieve will therefore contain primes up to', N)

def primes_up_to(N):
    """A generator yielding all primes less than N."""

    yield 2
    # Only consider odd numbers up to N, starting at 3
    bsieve = [True] * ((N-1)//2)
    for i,bp in enumerate(bsieve):
        p = 2*i + 3
        if bp:
            yield p
            # Mark off all multiples of p as composite
            for m in range(i, (N-1)//2, p):
                bsieve[m] = False

gen_primes = primes_up_to(N)
sieve = list(gen_primes)

def is_prime(n, imax):
    """Return True if n is prime, else return False.

    imax is the maximum index in the sieve of potential prime factors that
    needs to be considered; this should be the index of the first prime number
    larger than the square root of n.

    """
    return not any(n % p == 0 for p in sieve[:imax])


digit_count = {1: {1: 0, 3: 0, 7: 0, 9: 0},
               3: {1: 0, 3: 0, 7: 0, 9: 0},
               7: {1: 0, 3: 0, 7: 0, 9: 0},
               9: {1: 0, 3: 0, 7: 0, 9: 0}}

# nprimes is the number of prime numbers encountered
nprimes = 0
# the most recent prime number considered (we start with the first prime number
# which ends with 1,3,7 or 9 and is followed by a number ending with one of
# these digits, 7 since 2, 3 and 5 are somewhat special cases.
last_prime = 7
# The current prime number to consider, initially the one after 7 which is 11
n = 11
# The index of the maximum prime in our sieve we need to consider when testing
# for primality: initially 2, since sieve[2] = 5 is the nearest prime larger
# than sqrt(11). plim is this largest prime from the sieve.
imax = 2
plim = sieve[imax]
start_time = time.time()

while nprimes <= nmax:
    # Output a progress indicator
    if not nprimes % 1000:
        print(nprimes)

    if is_prime(n, imax):
        # n is prime: update the dictionary of last digits
        digit_count[last_prime % 10][n % 10] += 1
        last_prime = n
        nprimes += 1
    # Move on to the next candidate (skip even numbers)
    n += 2

    # Update imax and plim if necessary
    if math.sqrt(n) >= plim:
        imax += 1
        plim = sieve[imax]
end_time = time.time()
print(digit_count)
print('Time taken: {:.2f} s'.format(end_time - start_time))

The returned dictionary (formatted for clarity) is

{1: {1: 446808, 3: 756072, 7: 769924, 9: 526953},
 3: {1: 593196, 3: 422302, 7: 714795, 9: 769915},
 7: {1: 639384, 3: 681759, 7: 422289, 9: 756852},
 9: {1: 820369, 3: 640076, 7: 593275, 9: 446032}}

Plotting these data on a bar chart:

import numpy as np
import matplotlib.pyplot as plt

# First 10,000,000 primes
digit_count = {1: {1: 446808, 3: 756072, 9: 526953, 7: 769924},
               3: {1: 593196, 3: 422302, 9: 769915, 7: 714795},
               9: {1: 820369, 3: 640076, 9: 446032, 7: 593275},
               7: {1: 639384, 3: 681759, 9: 756852, 7: 422289}}

fig, ax = plt.subplots(nrows=2, ncols=2, facecolor='#dddddd')

xticks = [0,1,2,3]
last_digits = [1,3,7,9]
for i, d in enumerate(last_digits):
    ir, ic = i // 2, i % 2 
    this_ax = ax[ir,ic]
    this_ax.patch.set_alpha(1)
    count = np.array([digit_count[d][j] for j in last_digits])
    total = sum(count)
    prob = count / total * 100
    this_ax.bar(xticks, prob, align='center', color='maroon', ec='maroon',
                 alpha=0.7)
    this_ax.set_title('Last digit of prime: {:d}'.format(d), fontsize=14)
    this_ax.set_xticklabels(['{:d}'.format(j) for j in last_digits])
    this_ax.set_xticks(xticks)
    this_ax.set_yticks([0,10,20,30,40])
    this_ax.set_ylim(0,35)
    this_ax.set_yticks([])
    for j, pr in enumerate(prob):
        this_ax.annotate('{:.1f}%'.format(pr), xy=(j, pr), ha='center',
                         va='top', color='w', fontsize=12)
    this_ax.set_xlabel('Next prime ends in')
    this_ax.set_frame_on(False)
    this_ax.tick_params(axis='x', length=0)
    this_ax.tick_params(axis='y', length=0)
fig.subplots_adjust(wspace=0.2, hspace=0.7, left=0, bottom=0.1, right=1,
                    top=0.95)
plt.show()

The output seems to confirm the headline finding of Oliver and Soundararajan's article with approximately the same probabilities reported in the press for their larger prime number collection.

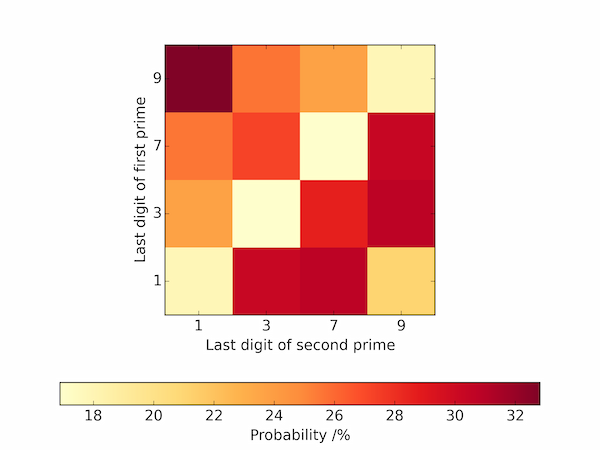
The following code visualizes these data as a heatmap of probabilities.

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import FuncFormatter

# First 10,000,000 primes
digit_count = {1: {1: 446808, 3: 756072, 9: 526953, 7: 769924},
               3: {1: 593196, 3: 422302, 9: 769915, 7: 714795},
               9: {1: 820369, 3: 640076, 9: 446032, 7: 593275},
               7: {1: 639384, 3: 681759, 9: 756852, 7: 422289}}
last_digits = [1,3,7,9]

hmap = np.empty((4,4))
for i, d1 in enumerate(last_digits):
    total = sum(digit_count[d1].values())
    for j, d2 in enumerate(last_digits):
        hmap[i,j] = digit_count[d1][d2] / total * 100

fig = plt.figure()
ax = fig.add_axes([0.1,0.3,0.8,0.6])
im = ax.imshow(hmap, interpolation='nearest', cmap=plt.cm.YlOrRd, origin='lower')
tick_labels = [str(d) for d in last_digits]
ax.set_xticks(range(4))
ax.set_xticklabels(tick_labels)
ax.set_xlabel('Last digit of second prime')
ax.set_yticks(range(4))
ax.set_yticklabels(tick_labels)
ax.set_ylabel('Last digit of first prime')

cbar_axes = fig.add_axes([0.1,0.1,0.8,0.05])

cbar = plt.colorbar(im, orientation='horizontal', cax=cbar_axes)
cbar.ax.set_xlabel('Probability /%')

plt.savefig('prime_digits_hmap.png')
plt.show()

There is a pleasing symmetry in this plot, particularly about the "anti-diagonal" which is mentioned but not fully explained in Oliver and Soundararajan's paper.