Cobweb plots
Posted on 01 November 2017
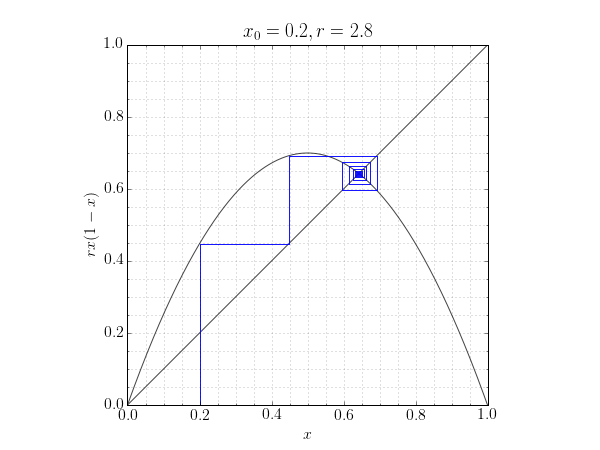
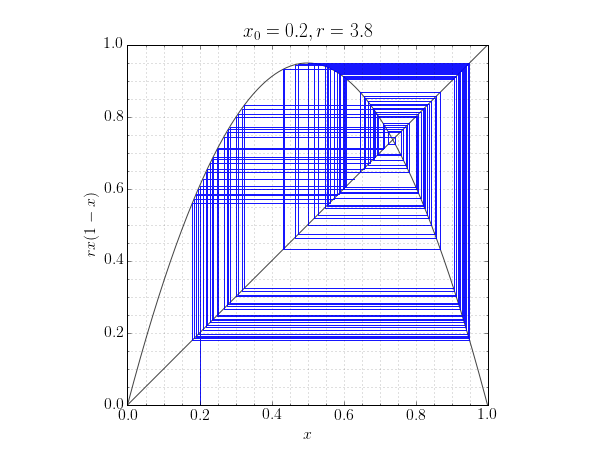
A cobweb plot is often used to visulaize the behaviour of an iterated function. That is, the sequence of values obtained from setting $x_{n+1} = f(x_n)$, starting at some value $x_0$.
The plot can reveal stable, cyclic, or chaotic behaviour as convergence to a point, a repeating rectangle or by filling the plane with non-repeating line segments respectively.
The code below generates a cobweb plot for the logistic map: $f(x) = rx(1-x)$. With a chosen starting value of $x_0=0.5$, both stable and chaotic behaviour is observed for different values of $r$.
import numpy as np
from matplotlib import rc
import matplotlib.pyplot as plt
# Use LaTeX throughout the figure for consistency
rc('font', **{'family': 'serif', 'serif': ['Computer Modern'], 'size': 16})
rc('text', usetex=True)
# Figure dpi
dpi = 72
def plot_cobweb(f, r, x0, nmax=40):
"""Make a cobweb plot.
Plot y = f(x; r) and y = x for 0 <= x <= 1, and illustrate the behaviour of
iterating x = f(x) starting at x = x0. r is a parameter to the function.
"""
x = np.linspace(0, 1, 500)
fig = plt.figure(figsize=(600/dpi, 450/dpi), dpi=dpi)
ax = fig.add_subplot(111)
# Plot y = f(x) and y = x
ax.plot(x, f(x, r), c='#444444', lw=2)
ax.plot(x, x, c='#444444', lw=2)
# Iterate x = f(x) for nmax steps, starting at (x0, 0).
px, py = np.empty((2,nmax+1,2))
px[0], py[0] = x0, 0
for n in range(1, nmax, 2):
px[n] = px[n-1]
py[n] = f(px[n-1], r)
px[n+1] = py[n]
py[n+1] = py[n]
# Plot the path traced out by the iteration.
ax.plot(px, py, c='b', alpha=0.7)
# Annotate and tidy the plot.
ax.minorticks_on()
ax.grid(which='minor', alpha=0.5)
ax.grid(which='major', alpha=0.5)
ax.set_aspect('equal')
ax.set_xlabel('$x$')
ax.set_ylabel(f.latex_label)
ax.set_title('$x_0 = {:.1}, r = {:.2}$'.format(x0, r))
plt.savefig('cobweb_{:.1}_{:.2}.png'.format(x0, r), dpi=dpi)
class AnnotatedFunction:
"""A small class representing a mathematical function.
This class is callable so it acts like a Python function, but it also
defines a string giving its latex representation.
"""
def __init__(self, func, latex_label):
self.func = func
self.latex_label = latex_label
def __call__(self, *args, **kwargs):
return self.func(*args, **kwargs)
# The logistic map, f(x) = rx(1-x).
func = AnnotatedFunction(lambda x,r: r*x*(1-x), r'$rx(1-x)$')
plot_cobweb(func, 2.8, 0.2)
plot_cobweb(func, 3.8, 0.2, 200)