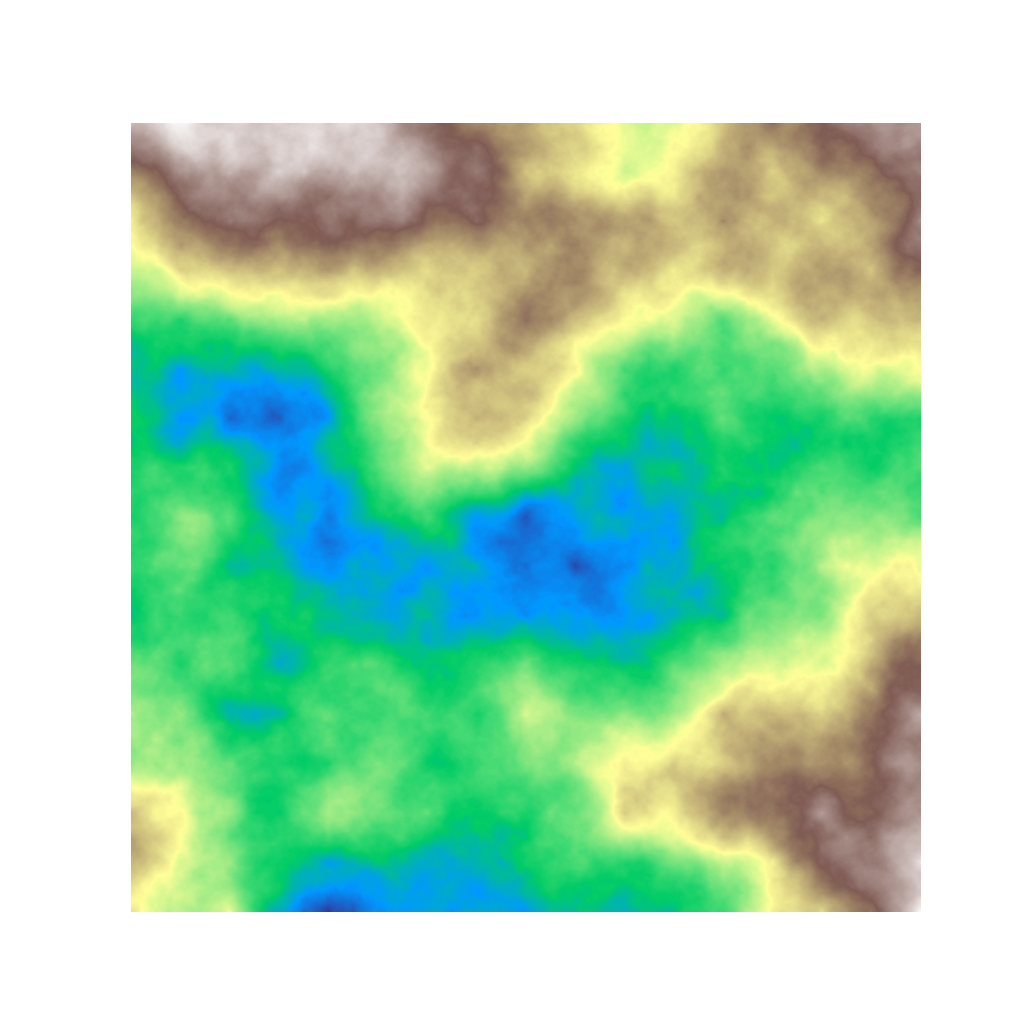
Cloud images using the diamond-square algorithm

import numpy as np
import matplotlib.pyplot as plt

# The array must be square with edge length 2**n + 1
n = 6
N = 2**n + 1
# f scales the random numbers at each stage of the algorithm
f = 1.0

# Initialise the array with random numbers at its corners
arr = np.zeros((N, N))
arr[0::N-1,0::N-1] = np.random.uniform(-1, 1, (2,2))
side = N-1

nsquares = 1
while side > 1:
    sideo2 = side // 2

    # Diamond step
    for ix in range(nsquares):
        for iy in range(nsquares):
            x0, x1, y0, y1 = ix*side, (ix+1)*side, iy*side, (iy+1)*side
            xc, yc = x0 + sideo2, y0 + sideo2
            # Set this pixel to the mean of its "diamond" neighbours plus
            # a random offset.
            arr[yc,xc] = (arr[y0,x0] + arr[y0,x1] + arr[y1,x0] + arr[y1,x1])/4
            arr[yc,xc] += f * np.random.uniform(-1,1)

    # Square step: NB don't do this step until the pixels from the preceding
    # diamond step have been set.
    for iy in range(2*nsquares+1):
        yc = sideo2 * iy
        for ix in range(nsquares+1):
            xc = side * ix + sideo2 * (1 - iy % 2)
            if not (0 <= xc < N and 0 <= yc < N):
                continue
            tot, ntot = 0., 0
            # Set this pixel to the mean of its "square" neighbours plus
            # a random offset. At the edges, it has only three neighbours
            for (dx, dy) in ((-1,0), (1,0), (0,-1), (0,1)):
                xs, ys = xc + dx*sideo2, yc + dy*sideo2
                if not (0 <= xs < N and 0 <= ys < N):
                    continue
                else:
                    tot += arr[ys, xs]
                    ntot += 1
            arr[yc, xc] += tot / ntot + f * np.random.uniform(-1,1)
    side = sideo2
    nsquares *= 2
    f /= 2

plt.imshow(arr, cmap=plt.cm.Blues)
plt.axis('off')
plt.show()