Posted by: christian on 24 Feb 2017
It is a standard result of statistical thermodynamics that the molar heat capacity at constant volume, $C_{V,\mathrm{m}}$, is related to the molecular partition sum, $q$, through the relation $$ C_{V,\mathrm{m}} = R\beta^2\left[\frac{\ddot{q}}{q} - \left( \frac{\dot{q}}{q}\right)^2\right], $$ where $\dot{q}$ and $\ddot{q}$ represent the first and second derivative of $q$ with respect to the "thermodynamic beta", $\beta = \frac{1}{k_\mathrm{B}T}$:
\begin{align*} q &= \sum_i g_i e^{-\beta \epsilon_i}\\ \dot{q} \equiv \left( \frac{\partial q}{\partial \beta}\right)_V &= - \sum_i \epsilon_i g_i e^{-\beta \epsilon_i}\\ \ddot{q} \equiv \left( \frac{\partial^2 q}{\partial \beta^2}\right)_V &= \sum_i \epsilon_i^2 g_i e^{-\beta \epsilon_i} \end{align*}
There are several numerical issues to be dealt with in the evaluation of these summations. For example, it is not always easy to determine when convergence has been reached, and the fact that the terms can become very small as $i$ increases means that it is easy to introduce artefacts related to the finite-precision floating point representation of real numbers.
The code below defines a function calc_sum to sum a general series provided in the iterable object get_term. It uses Python's math.fsum to avoid the loss of floating point precision by tracking intermediate partial sums (the Shewchuk algorithm).
The individual functions calc_q, calc_qdot and calc_qdotdot then call calc_sum, passing it beta and user-provided functions to calculate the energy, $\epsilon_i$ (Efunc) and degeneracy, $g_i$ (gfunc) of the $i$th energy level. These, in turn, are called by calc_CV which calculates the heat capacity. Any additional arguments (such as molecular constants) that Efunc and gfunc need should be passed in the tuple args to this function.
import numpy as np
from scipy.constants import h, c, k as kB, R
# Speed of light in cm.s-1
c *= 100
hc = h * c
def calc_sum(get_term, max_terms=500, TINY=1.e-100):
"""Sum a finite or absolutely convergent series to convergence.
The terms in the series are returned by the get_term iterator. No more than
max_terms are summed, and convergence is assumed when a term is not zero
but smaller than TINY.
"""
terms = []
for i in range(max_terms):
try:
term = next(get_term)
except StopIteration:
break
if term and term < TINY:
break
terms.append(term)
else:
if terms[-1] >= TINY:
print('Warning: maximum number of iterations reached in calc_sum.')
return np.math.fsum(terms)
def get_term(beta, gfunc, Efunc, calc_term, args=()):
"""A generator returning each term in the partition sum or its derivative.
The energy and degeneracy for the ith term are returned by Efunc and gfunc
respectively. Any arguments they require beyond i should be passed in the
tuple args. If Efunc should return None to signal the end of the series.
The function calc_term should calculate the term given beta, g and E.
"""
i = 0
while True:
E = Efunc(i, *args)
if E is None:
return None
yield calc_term(beta, gfunc(i, *args), E)
i += 1
def calc_q_term(beta, g, E):
"""Return a term from the partition sum.
beta = (kB.T)^-1 in J, g is the degeneracy and E, the energy, is in cm-1.
"""
return g * np.exp(-E * h * c * beta)
def calc_qdot_term(beta, g, E):
"""Return a term from the first derivative of partition sum wrt beta.
beta = (kB.T)^-1 in J, g is the degeneracy and E, the energy, is in cm-1.
The qdot=dq/dbeta term is returned in units of cm-1.
"""
return E * calc_q_term(beta, g, E)
def calc_qdotdot_term(beta, g, E):
"""Return a term from the second derivative of partition sum wrt beta.
beta = (kB.T)^-1 in J, g is the degeneracy and E, the energy, is in cm-1.
The qdotdot=d2q/dbeta2 term is returned in units of cm-2.
"""
return E * calc_qdot_term(beta, g, E)
def calc_q(beta, gfunc, Efunc, args=()):
"""Return the partition sum, q, at beta = (kB.T)^-1.
gfunc and Efunc are functions returning the degeneracy and energy of the
ith term in the partition sum. Any arguments they require beyond i should
be passed in the tuple args.
"""
return calc_sum(get_term(beta, gfunc, Efunc, calc_q_term, args))
def calc_qdot(beta, gfunc, Efunc, args=()):
"""Return the first derivative partition sum at beta = (kB.T)^-1.
gfunc and Efunc are functions returning the degeneracy and energy of the
ith term in the partition sum. Any arguments they require beyond i should
be passed in the tuple args. qdot = dq/dbeta is returned in units of J
"""
return - hc * calc_sum(get_term(beta, gfunc, Efunc, calc_qdot_term, args))
def calc_qdotdot(beta, gfunc, Efunc, args=()):
"""Return the second derivative of the partition sum at beta = (kB.T)^-1.
gfunc and Efunc are functions returning the degeneracy and energy of the
ith term in the partition sum. Any arguments they require beyond i should
be passed in the tuple args. qdotdot = d2q/dbeta2 is returned in units
of J^2.
"""
return hc**2 * calc_sum(get_term(beta, gfunc, Efunc, calc_qdotdot_term,
args))
def calc_qfuncs(Tgrid, gfunc, Efunc, args=()):
"""Calculate the partition sum and its first two derivatives on Tgrid.
gfunc and Efunc are functions returning the degeneracy and energy of the
ith term in the partition sum. Any arguments they require beyond i should
be passed in the tuple args.
"""
q = np.zeros_like(Tgrid)
qdot = np.zeros_like(Tgrid)
qdotdot = np.zeros_like(Tgrid)
for i,T in enumerate(Tgrid):
beta = 1/kB/T
q[i] = calc_q(beta, gfunc, Efunc, args)
qdot[i] = calc_qdot(beta, gfunc, Efunc, args)
qdotdot[i] = calc_qdotdot(beta, gfunc, Efunc, args)
return q, qdot, qdotdot
def calc_CV(Tgrid, gfunc, Efunc, args=()):
"""Calculate the heat capacity, CV, on the grid of temperatures, Tgrid.
The Tgrid should be a sequence of temperatures in K.
gfunc and Efunc are functions returning the degeneracy and energy of the
ith term in the partition sum. Any arguments they require beyond i should
be passed in the tuple args.
The heat capacity at constant volume, CV, is returned in J.K-1.mol-1.
"""
beta = 1 / kB / Tgrid
q, qdot, qdotdot = calc_qfuncs(Tgrid, gfunc, Efunc, args)
return R * beta**2 * (qdotdot/q - (qdot/q)**2)
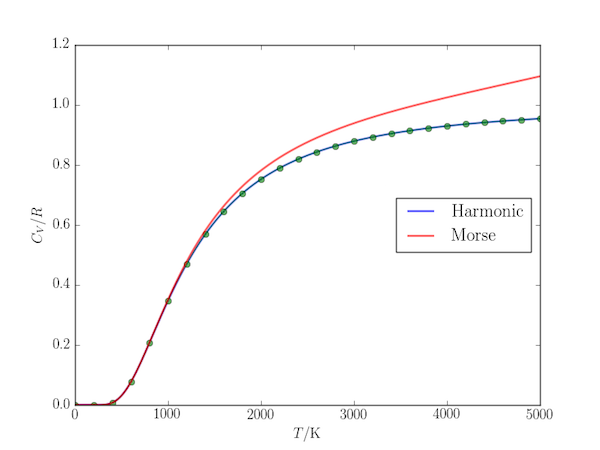
As an example of its usage, here is a comparison of the vibrational contribution to the heat capacity of the HBr molecule using (a) the harmonic approximation and (b) the Morse approximation to its energy levels. The harmonic approximation values are also compared with their values obtained from the analytical expression $$ C_{V,\mathrm{m}}(\mathrm{sho}) = \frac{Rx^2e^{-x}}{(1+e^-x)^2}, $$ where $x=\beta h c \tilde{\nu}$ and $\tilde{\nu}$ is the harmonic vibrational wavenumber.
import numpy as np
from scipy.constants import h, c, k as kB, R
# Speed of light in cm.s-1
c *= 100
hc = h * c
import matplotlib.pyplot as plt
from matplotlib import rc
from partition_function import calc_CV
rc('font', **{'family': 'serif', 'serif': ['Computer Modern'], 'size': 14})
rc('text', usetex=True)
# Morse parameters for HBr, cm-1
we, wexe = 2648.975, 45.217
# Maximum quantum number v within Morse approximation
vmax = int(we/2/wexe)
print(vmax)
# Approximate harmonic vibrational wavenumber, cm-1
nu = we - wexe
# Temperature grid, K
T = np.linspace(1,5000,501)
# To get a feel for how many vibrational levels are thermally accessible,
# calculate the Harmonic approximation partition sum
Tmax = T[-1]
qsho_max = 1./(1-np.exp(-hc*nu/kB/Tmax))
print('q_sho({} K) = {}'.format(Tmax, qsho_max))
# Functions for calculating terms in the partition sum and its derivatives
def gvib(v, *args):
# Vibrational energy levels of closed-shell diatomics are non-degenerate.
return 1
def Esho(v, nu):
"""Return the Harmonic approximation energy for v, with E=0 for v=0."""
return nu * v
def Emorse(v, we, wexe, vmax):
"""Return the Morse approximation energy for v, with E=0 for v=0."""
if v > vmax:
return None
return we * v - wexe * v**2
CVsho = calc_CV(T, gvib, Esho, args=(nu,))
CVmorse = calc_CV(T, gvib, Emorse, args=(we, wexe,vmax))
x = hc*nu/kB/T
CVsho_analytical = R * x**2 * np.exp(-x)/(1-np.exp(-x))**2
plt.plot(T, CVsho/R, label="Harmonic", lw=2, alpha=0.6)
plt.plot(T, CVsho_analytical/R, marker='o', markevery=20, alpha=0.6)
plt.plot(T, CVmorse/R, label="Morse", lw=2, alpha=0.6)
plt.legend(loc=5)
plt.xlabel(r'$T/\mathrm{K}$')
plt.ylabel(r'$C_V/R$')
plt.savefig('HBr-CV.png')
plt.show()
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
There are currently no comments
New Comment