Posted by: christian on 30 Sep 2023
A recent tweet by @iwontoffendyou posed the following problem: with reference to the figure below, what is the radius of the orange circle, which is tangent to the $y$-axis, the unit circle and the curve $y = \sqrt{x}$?
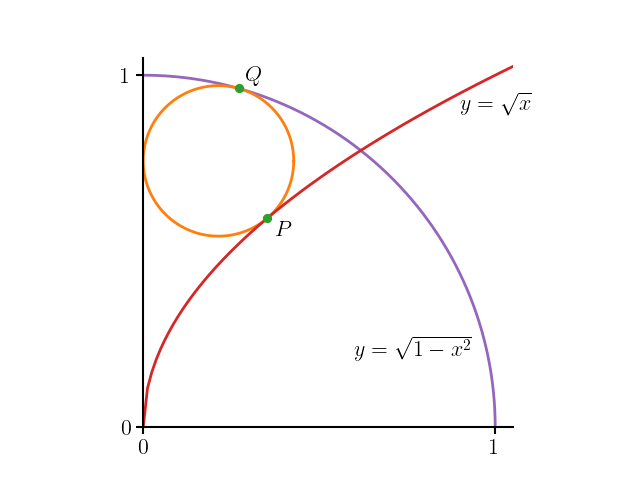
Here are two ways to solve this problem using SymPy, Python's symbolic computation library.
Method 1
Let the centre of the small circle be $(r, b)$ (the $x$-coordinate of its centre must be $r$ because it is tangent to the $y$-axis. The equation of this circle is therefore
$$ (x-r)^2 + (y-b)^2 = r^2 $$
At the point $Q$ the small circle is tangent to the unit circle: let $Q=(d, \sqrt{1-d^2})$, where:
$$ (d-r)^2 + \left[\sqrt{1-d^2} - b\right]^2 = r^2 $$
The gradients of the purple and orange curves are:
\begin{align} y' = \frac{-x}{\sqrt{1-x^2}}\\ 2(x-r) + 2(y-b)y' = 0 \Rightarrow y' = \frac{r-x}{y-b}. \end{align}
and these are equal at $x=d$, so
$$ d\left[\sqrt{1-d^2}-b\right] = (d-r)\sqrt{1-d^2}. $$
SymPy can solve this pair of equations for $d$ and $r$ in terms of (the still unknown) $b$ straight away:
import sympy as sp
r, b, c, d = sp.symbols("r b c d", positive=True, real=True)
E1 = (d - r)**2 + (sp.sqrt(1 - d**2) - b)**2 - r**2
E2 = d * (sp.sqrt(1 - d**2) - b) - (d - r) * sp.sqrt(1 - d**2)
soln1 = sp.solve([E1, E2], [r, d], dict=True)
soln1
[{d: sqrt(b**4 - 2*b**2 + 1)/(b**2 + 1), r: sqrt(b**4 - 2*b**2 + 1)/2}]
That is,
$$ d = \frac{\sqrt{b^4-2b^2+1}}{b^2+1}, \; r = \frac{1}{2}\sqrt{b^4-2b^2+1}. $$
At the point $P$ the small circle is tangent to the curve $y=\sqrt{x}$. Let $P=(c,\sqrt{c})$, so
$$ (c-r)^2+\left(\sqrt{c}-b\right)^2 = r^2 $$
and from the gradient of the red line,
$$ y' = \frac{1}{2\sqrt{x}} $$
at $x=c$ we have
$$ \frac{1}{2\sqrt{c}} = \frac{r-c}{\sqrt{c}-b} \Rightarrow \sqrt{c} - b = 2\sqrt{c}(r-c). $$
This pair of equations can also be solved (for $b$ and $c$)
E3 = (c - r)**2 + (sp.sqrt(c) - b)**2 - r**2
E4 = sp.sqrt(c) - b - 2 * sp.sqrt(c) * (r - c)
soln2 = sp.solve([E3, E4], [b, c], dict=True)
soln2
[{b: (3/16 - sqrt(16*r + 1)/16)*sqrt(16*r - 2*sqrt(16*r + 1) - 2),
c: r - sqrt(16*r + 1)/8 - 1/8},
{b: (sqrt(16*r + 1)/16 + 3/16)*sqrt(16*r + 2*sqrt(16*r + 1) - 2),
c: r + sqrt(16*r + 1)/8 - 1/8}]
This time there are two solutions (equations for $b$ in terms of $r$), and solving each of these gives a total of four equations for $r$:
b1 = soln2[0][b]
r1 = sp.solve(soln1[0][r].subs(b, b1) - r, r)
r1
[1/2,
11/8 + sqrt(227/(96*(251*sqrt(3765)/9216 + 2159/1024)**(1/3)) + 2*(251*sqrt(3765)/9216 + 2159/1024)**(1/3) + 145/16)/2 + sqrt(-2*(251*sqrt(3765)/9216 + 2159/1024)**(1/3) - 227/(96*(251*sqrt(3765)/9216 + 2159/1024)**(1/3)) + 1631/(32*sqrt(227/(96*(251*sqrt(3765)/9216 + 2159/1024)**(1/3)) + 2*(251*sqrt(3765)/9216 + 2159/1024)**(1/3) + 145/16)) + 145/8)/2]
b2 = soln2[1][b]
r2 = sp.solve(soln1[0][r].subs(b, b2) - r, r)
r2
[-1 - 25/(12*(75/16 + 175*sqrt(21)/144)**(1/3)) + (75/16 + 175*sqrt(21)/144)**(1/3),
-sqrt(-2*(251*sqrt(3765)/9216 + 2159/1024)**(1/3) - 227/(96*(251*sqrt(3765)/9216 + 2159/1024)**(1/3)) + 1631/(32*sqrt(227/(96*(251*sqrt(3765)/9216 + 2159/1024)**(1/3)) + 2*(251*sqrt(3765)/9216 + 2159/1024)**(1/3) + 145/16)) + 145/8)/2 + 11/8 + sqrt(227/(96*(251*sqrt(3765)/9216 + 2159/1024)**(1/3)) + 2*(251*sqrt(3765)/9216 + 2159/1024)**(1/3) + 145/16)/2]
The four solutions can be plot together for comparison:
import numpy as np
import matplotlib.pyplot as plt
def make_plot(ax, r, b):
th = np.linspace(0, 2 * np.pi, 100)
x1, y1 = np.cos(th), np.sin(th)
x2 = np.linspace(0, 10, 1000)
y2 = np.sqrt(x2)
ax.plot(x1, y1, c='tab:purple')
ax.plot(x2, y2, c='tab:red')
x3, y3 = r * np.cos(th) + r, r * np.sin(th) + b
ax.plot(x3, y3, c='tab:orange')
ax.axis("square")
fig, axes = plt.subplots(nrows=2, ncols=2)
make_plot(axes[0][0], r1[0].evalf(), b1.subs(r, r1[0]).evalf())
make_plot(axes[0][1], r1[1].evalf(), b1.subs(r, r1[1]).evalf())
make_plot(axes[1][0], r2[0].evalf(), b2.subs(r, r2[0]).evalf())
make_plot(axes[1][1], r2[1].evalf(), b2.subs(r, r2[1]).evalf())
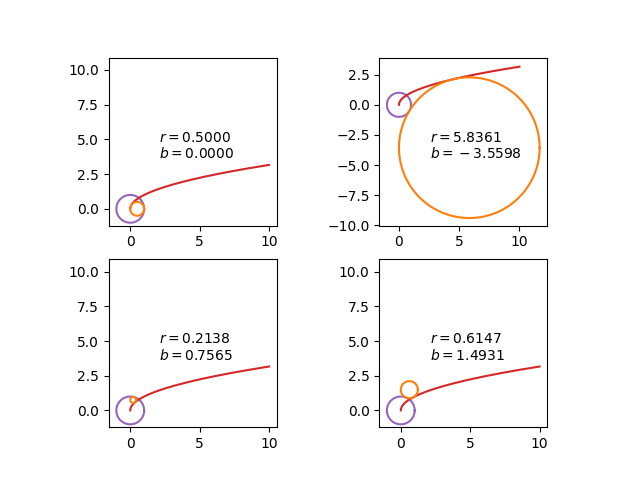
These all satisfy the condition that the orange circle should be tangent to the $y$ axis, the unit circle and the curve $y=\sqrt{x}$, but from the figure provided in the statement of the problem, it is clear that the required solution (with the orange circle within the unit circle and above the parabola) is
r2[0]
$$ \displaystyle -1 - \frac{25}{12 \sqrt[3]{\frac{75}{16} + \frac{175 \sqrt{21}}{144}}} + \sqrt[3]{\frac{75}{16} + \frac{175 \sqrt{21}}{144}} $$
and the centre of the circle is at coordinates:
r2[0].evalf(), b2.subs(r, r2[0]).evalf()
(0.213841779235356, 0.756515988944906)
Method 2
An alternative solution was given by Twitter user @tiozzo_giulio. First write the condition for the small orange circle to touch the unit circle as
$$ \sqrt{r^2 + b^2} + r = 1 \rightarrow b^2 = 1 - 2r. $$
Substituting into the equation of the small circle, $(x-r)^2 + (y-b)^2 = r^2$ gives:
$$ x^2 + (b^2-1)x + (y-b)^2 = 0. $$
Now, for the red parabola, $x=y^2$, so, substituting this in eliminates $x$. After simplifying,
$$ y^4 + b^2y^2 - 2by + b^2 = 0. $$
For the circle to be tangent to both curves, we need the double root of this polynomial and its derivative. This is their resultant, provided by the determinant of the Sylvester Matrix:
import sympy as sp
from sympy.polys import subresultants_qq_zz
y, b, r = sp.symbols("y b r", positive=True, real=True)
f = y**4 + b**2 * y**2 - 2*b*y + b**2
fp = f.diff(y)
M = subresultants_qq_zz.sylvester(f, fp, y)
M
$$ \displaystyle \left[\begin{matrix}1 & 0 & b^{2} & - 2 b & b^{2} & 0 & 0\\0 & 1 & 0 & b^{2} & - 2 b & b^{2} & 0\\0 & 0 & 1 & 0 & b^{2} & - 2 b & b^{2}\\4 & 0 & 2 b^{2} & - 2 b & 0 & 0 & 0\\0 & 4 & 0 & 2 b^{2} & - 2 b & 0 & 0\\0 & 0 & 4 & 0 & 2 b^{2} & - 2 b & 0\\0 & 0 & 0 & 4 & 0 & 2 b^{2} & - 2 b\end{matrix}\right] $$
M.det()
$$ \displaystyle 16 b^{10} - 144 b^{8} + 832 b^{6} - 432 b^{4} $$
Substituting $b^2 = 1-2r$ and finding the roots gives:
eqn = M.det().subs(b**2, 1-2*r)
roots = sp.roots(eqn) roots
{1/2: 2,
-1 - 25/(12*(75/16 + 175*sqrt(21)/144)**(1/3)) + (75/16 + 175*sqrt(21)/144)**(1/3): 1,
-1 - 25/(12*(-1/2 + sqrt(3)*I/2)*(75/16 + 175*sqrt(21)/144)**(1/3)) + (-1/2 + sqrt(3)*I/2)*(75/16 + 175*sqrt(21)/144)**(1/3): 1,
-1 + (-1/2 - sqrt(3)*I/2)*(75/16 + 175*sqrt(21)/144)**(1/3) - 25/(12*(-1/2 - sqrt(3)*I/2)*(75/16 + 175*sqrt(21)/144)**(1/3)): 1}
Discarding the imaginary roots yields:
for root in roots:
if root.is_real:
print(root.evalf())
0.500000000000000
0.213841779235356
which are the two solutions found previously for which the small circle is contained within the unit circle.
Share on Twitter Share on Facebook
Comments
Comments are pre-moderated. Please be patient and your comment will appear soon.
jakal 1 year ago
\begin{align}
Link | Replyy' = \frac{-x}{\sqrt{1-x^2}}\\
2(x-r) + 2(y-b)y' = 0 \Rightarrow y' = \frac{r-x}{y-b}.
\end{align}
christian 1 year ago
Thanks – corrected.
Link | ReplyNew Comment