E31.3: Simulated Rovibrational Spectra of Diatomics

The file diatomic-data.tab contains parameters, in \(\mathrm{cm^{-1}}\), describing the energy levels of a selection of diatomic molecules. These energies can be written in the form:

$$ S(v, J) = G(v) + F(v, J), $$

where the anharmonic vibrational energies are parameterised as:

$$ G(v) = \textstyle\omega_\mathrm{e}\left(v + \frac{1}{2}\right) - \omega_\mathrm{e}x_\mathrm{e}\left(v + \frac{1}{2}\right)^2 + \omega_\mathrm{e}y_\mathrm{e}\left(v + \frac{1}{2}\right)^3 $$

and the rotational energies include centrifugal distortion and vibration-rotation interaction terms:

\begin{align*} F(v, J) & = B_vJ(J+1) - D_v[J(J+1)]^2\\ B_v &= \textstyle B_\mathrm{e} - \alpha_\mathrm{e}\left(v +\frac{1}{2}\right) + \gamma_\mathrm{e}\left(v +\frac{1}{2}\right)^2\\ D_v &= \textstyle D_\mathrm{e} - \beta_\mathrm{e}\left(v +\frac{1}{2}\right) \end{align*}

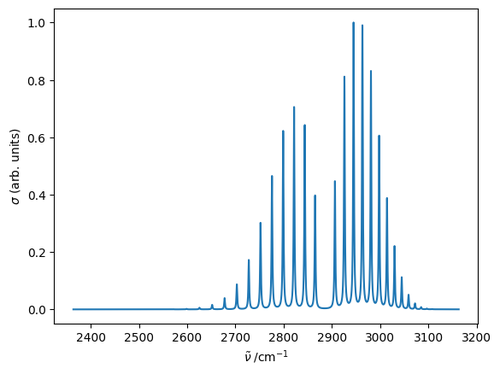
In this example, we will use these data to plot the rovibrational (IR) spectrum of the fundamental band (\(v=1 \leftarrow 0\)) of \(\mathrm{{}^1H^{35}Cl}\).

Some definitions, library imports and some useful physical constants from SciPy's physical_constants module:

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

from scipy.constants import physical_constants
# The second radiation constants, c2 = hc/kB, in cm.K
c2 = physical_constants['second radiation constant'][0] * 100
# Speed of light (m.s-1), atomic mass constant (kg) and Boltzmann constant (J.K-1)
c = physical_constants['speed of light in vacuum'][0]
u = physical_constants['atomic mass constant'][0]
kB = physical_constants['Boltzmann constant'][0]

The data are in fixed-width fields, separated by whitespace, with the asterisk character used as a placeholder for missing values.

df = pd.read_csv('diatomic-data.tab', sep='\s+', index_col=0, na_values='*')
df

            (12C)(16O)   (1H)(35Cl)  ...   (1H)(81Br)       (16O)2
parameter                            ...                          
we         2169.813600  2990.946300  ...  2648.975000  1580.193000
wexe         13.288310    52.818600  ...    45.217500    11.981000
weye               NaN     0.224370  ...    -0.002900     0.047470
Be            1.931281    10.593416  ...     8.464884     1.437677
alpha_e       0.017504     0.307181  ...     0.233280     0.015930

[5 rows x 6 columns]

First we are going to need a function to calculate the energy (in \(\mathrm{cm^{-1}}\)) of a rovibrational state using the above formula for \(S(v, J)\).

def get_E(v, J, molecule):
    """Return the energy, in cm-1, of the state (v, J) for a molecule."""

    # Get the parameters, replacing NaN values with 0
    prms = df[molecule].fillna(0)
    vfac, Jfac = v + 0.5, J * (J+1)
    Bv = prms['Be'] - prms['alpha_e'] * vfac + prms['gamma_e'] * vfac**2
    Dv = prms['De'] - prms['beta_e'] * vfac
    F = Bv * Jfac - Dv * Jfac**2
    G = prms['we'] * vfac - prms['wexe'] * vfac**2 + prms['weye'] * vfac**3
    return G + F

Next, identify the molecule by the column heading in the prms DataFrame, and decide how many energy levels to calculate; here up to \(J=50\) for each of the vibrational states, \(v=0,1,2\). These energy levels, and their degeneracies (\(2J+1\)) are stored in a new DataFrame called states, with a MultiIndex: each row is identified by the tuple (v, J).

T = 296
molecule = '(1H)(35Cl)'
states_vmax, states_Jmax = 2, 50
index = pd.MultiIndex.from_tuples(
    ((v, J) for v in range(states_vmax+1) for J in range(states_Jmax+1)),
    names=['v', 'J'])
states = pd.DataFrame(index=index, columns=('E', 'g'), dtype=float)
for v, J in index:
    # Set the energy and the degeneracy columns.
    states.loc[(v, J), 'E'] = get_E(v, J, molecule)
    states.loc[(v, J), 'g'] = 2 * J + 1
# Convert the dtype of the degeneracy column to int.
states = states.convert_dtypes()
states

                 E    g
v J                    
0 0    1482.296546    1
  1    1503.174069    3
  2    1544.916349    5
  3    1607.497853    7
  4     1690.88028    9
...            ...  ...
2 46  25906.990015   93
  47  26609.673157   95
  48  27317.604419   97
  49  28030.171006   99
  50  28746.747356  101

[153 rows x 2 columns]

Calculate the partition sum, \(q\), from the calculated state energies and degeneracies.

E, g = states['E'], states['g']
E0 = get_E(0, 0, molecule)
# In the partition sum, measure energies from the zero-point level.
q = np.sum(g * np.exp(-c2 * (E - E0) / T))

In calculating the transitions, it is not necessary to use all of the states above (since the higher-\(J\) energy levels will be barely populated at this temperature and the line strengths correspondingly small): set a new rotational quantum number maximum for calculating the spectrum, and construct a new DataFrame to hold the transition data. For a closed-shell diatomic molecule there are two branches to the rovibrational spectrum, \(P(J'')\) and \(R(J'')\), corresponding to \(\Delta J = J' - J'' = -1\) and \(+1\), respectively. The index for this DataFrame will be a string corresponding to this designation.

trans_Jmax = 20
Jpp_P = np.arange(trans_Jmax, 0, -1)
Jpp_R = np.arange(0, trans_Jmax)
Pbranch = [f'P({Jpp})' for Jpp in Jpp_P]
Rbranch = [f'R({Jpp})' for Jpp in Jpp_R]
trans = pd.DataFrame(index=np.concatenate((Pbranch, Rbranch)))
trans['Jpp'] = np.concatenate((Jpp_P, Jpp_R))
trans['Jp'] = np.concatenate((Jpp_P-1, Jpp_R+1))
vp, vpp = 1, 0

Now iterate over the values of \(J''\) and \(J'\), calculating the transition wavenumber and relative line strengths from the energies in the states table. The line strengths are given by

$$ S \propto \tilde{\nu}_0 \frac{H(J'')}{q}\exp\left(-\frac{c_2 E''}{T}\right)\left[ 1 - \exp\left(-\frac{c_2 \tilde{\nu}_0}{T}\right)\right], $$

where \(H(J'')\) is a Hönl-London factor equal to \(J''+1\) for the R-branch lines and \(J''\) for the P-branch.

for br, (Jpp, Jp) in trans[['Jpp', 'Jp']].iterrows():
    # Store the transition's upper and lower state energies in the trans table,
    # measured from the zero-point level.
    Epp = states.loc[(vpp, Jpp), 'E'] - E0
    Ep = states.loc[(vp, Jp), 'E'] - E0
    nu = Ep - Epp
    # Also calculate the relative intensity, including a Honl-London factor,
    # P-branch: H(J") = J", R-branch: H(J") = J"+1
    HLfac = Jpp
    if Jp - Jpp == 1:
        HLfac = Jpp + 1
    rS = nu * HLfac / q * np.exp(-c2 * Epp / T) * (1 - np.exp(-c2 * nu / T))
    trans.loc[br, ['Epp', 'Ep', 'nu0', 'rS']] = Epp, Ep, nu, rS

trans.head()

       Jpp  Jp          Epp           Ep          nu0        rS
P(20)   20  19  4290.892494  6659.631076  2368.738583  0.000002
P(19)   19  18  3890.321554  6289.184891  2398.863337  0.000014
P(18)   18  17  3508.202491  5936.818786  2428.616295  0.000086
P(17)   17  16  3144.777869  5602.762558  2457.984688  0.000478
P(16)   16  15  2800.277487  5287.233239  2486.955751  0.002430

To calculate a spectrum, first establish a grid of wavenumber points covering the range of transition frequencies (with a bit of padding).

# Maximum and minimum transition wavenumbers.
numin, numax = trans['nu0'].min(), trans['nu0'].max()
# Pad the wavenumber grid by 5 cm-1 at each end
numin, numax = round(numin) - 5, round(numax) + 5
nu = np.arange(numin, numax, 0.001)

Also define some normalized lineshape functions: a Gaussian profile, \(f_\mathrm{G}\) (for Doppler broadening) and a Lorentzian profile, \(f_\mathrm{L}\) (for where pressure-broadening dominates), in terms of their respective half-widths at half-maximum (HWHM), \(\alpha_\mathrm{D}\) and \(\gamma_\mathrm{L}\):

\begin{align*} f_\mathrm{G}(\tilde{\nu}; \tilde{\nu}_0, \alpha_\mathrm{D}) & = \sqrt{\frac{\ln 2}{\alpha_\mathrm{D}^2\pi}} \exp\left[ -\ln 2\frac{(\tilde{\nu} - \tilde{\nu}_0)^2}{\alpha_\mathrm{D}^2}\right],\\ f_\mathrm{L}(\tilde{\nu}; \tilde{\nu}_0, \gamma_\mathrm{L}) & = \frac{\gamma_\mathrm{L}/\pi}{(\tilde{\nu} - \tilde{\nu}_0)^2 + \gamma_\mathrm{L}^2}. \end{align*}

def fG(nu, nu0, alphaD):
    """Normalized Gaussian function with HWHM alphaD, centered on nu0."""
    N = np.sqrt(np.log(2) / np.pi) / alphaD
    return N * np.exp(-np.log(2) * ((nu - nu0) / alphaD)**2)

def fL(nu, nu0, gammaL):
    """Normalized Lorentzian function with HWHM gammaL, centered on nu0."""
    N = 1 / np.pi
    return N * gammaL / ((nu - nu0)**2 + gammaL**2)

Set the Gaussian and Lorentzian HWHM values, \(\alpha_\mathrm{D}\) and \(\gamma_\mathrm{L}\) below. At 296 K, the Doppler width for HCl is small (about \(0.003\;\mathrm{cm^{-1}}\)), so here we will set a large-ish value for the pressure broadened width and use that.

# Molecular mass of (1H)(35Cl)
m = (1 + 35) * u
alphaD = nu.mean() / c * np.sqrt(2 * np.log(2) * kB * T / m)

gammaL = 1

Finally, calculate the contribution to the spectrum from each line and normalize to the maximum intensity.

spec = np.zeros_like(nu)
for br, row in trans.iterrows():
    spec += row['rS'] * fL(nu, row['nu0'], gammaL)
spec /= spec.max()

plt.plot(nu, spec)
plt.xlabel(r'$\tilde{\nu}\;/\mathrm{cm^{-1}}$')
plt.ylabel(r'$\sigma$ (arb. units)')