Transforming the molecular kinetic energy operator to an origin at the molecular centre of mass
The molecular kinetic energy operator for a diatomic molecule may be written
$$ T = -\sum_{\alpha=1}^2\frac{1}{2M_\alpha}P_\alpha^2 + \frac{1}{2m} \sum_{i=1}^n P_i^2 $$
where \(\mathbf{P}_{\alpha} = -i\hbar \nabla_{\alpha}\) and \(\mathbf{P}_i = -i\hbar \nabla_i \) are the momentum operators for the two nuclei and \(n\) electrons, respectively. \(M_\alpha\) are the masses of the nuclei and \(m\) is the electron mass. The vector differential operator del is
$$ \nabla_i = \mathbf{i}\frac{\partial}{\partial X_i} + \mathbf{j}\frac{\partial}{\partial Y_i} + \mathbf{k}\frac{\partial}{\partial Z_i}, $$
\(\mathbf{i}, \mathbf{j}\) and \(\mathbf{k}\) being the unit vectors along the \(X, Y\) and \(Z\) axes such that the position of the \(i\)th electron is \(\mathbf{R}_i = X_i\mathbf{i} + Y_i\mathbf{j} + X_i\mathbf{k}\) (and similarly for the nuclei).
Transformation from a space-fixed axis system with an arbitrary origin to one with the origin at the centre of mass of the molecule allows the translational motion of the whole molecule to be separated from its internal motion (rigorously, in the case of field-free space).
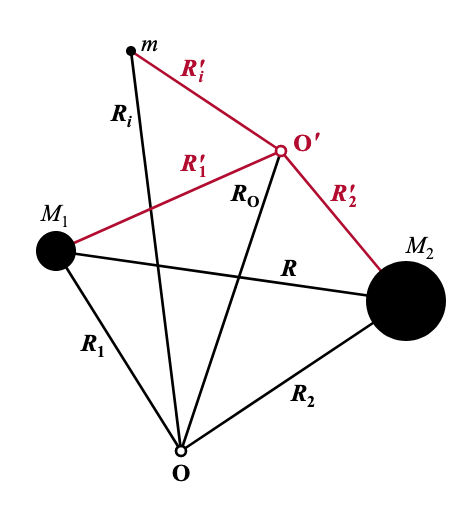
The coordinate system transformation from an arbitrary space-fixed origin (O, unprimed vectors) to one with its origin at the molecular centre of mass (O', primed vectors).
In these new coordinates the position vectors of the electrons and nuclei are:
$$ \mathbf{R}'_i = \mathbf{R}_i - \mathbf{R}_\mathrm{O} \quad \mathrm{and}\quad \mathbf{R}'_\alpha = \mathbf{R}_\alpha - \mathbf{R}_\mathrm{O} $$
where
$$ \mathbf{R}_\mathrm{O} = \frac{1}{M} \left[ m \sum_i \mathbf{R}_i + \sum_\alpha M_\alpha \mathbf{R}_\alpha \right] $$
is the position of the molecular centre of mass in the original coordinate system and
$$ M = nm + \sum_\alpha M_\alpha $$
is the total mass of the molecule (electrons and nuclei). Now, the new system of position vectors, \(\mathbf{R}'_i\) and \(\mathbf{R}'_\alpha\) represent \(3n+6\) coordinates referred to the centre of mass plus an additional three centre of mass corrdinates (\(\mathbf{R}'_\mathrm{O}\)). Therefore, three of these spatial coordinates are redundant: for example, the relation
$$ m\sum_i \mathbf{R}'_i + \sum_\alpha M_\alpha \mathbf{R}'_\alpha = 0 $$
can readily be shown to hold from the definition of \(\mathbf{R}'_i\) and \(\mathbf{R}'_\alpha\). We can remove this redundancy by considering the intermolecular vector \(\mathbf{R} = \mathbf{R}'_2 - \mathbf{R}'_1 = \mathbf{R}_1 - \mathbf{R}_2\) instead of the vectors \(\mathbf{R}'_1\) and \(\mathbf{R}'_2\) separately.
The transformation to molecular centre of mass coordinates therefore involved a change from the set of coordinates \(\mathbf{R}_i\) and \(\mathbf{R}_\alpha\) to the new set of coordinates \(\mathbf{R}'_i\), \(\mathbf{R}_\mathrm{O}\) and \(\mathbf{R}\). Correspondingly, the kinetic energy operator must be rewritten in terms of the momenta conjugate to these coordinates: respectively, \(\mathbf{P}'_i\), \(\mathbf{P}_\mathrm{O}\) and \(\mathbf{P}_R\). In its original form, this was written in terms of $P_i^2$ and $P_\alpha^2$. From the chain rule,
$$ \mathbf{P}_i = (\nabla_i \cdot \mathbf{R}_\mathrm{O}) \mathbf{P}_\mathrm{O} + (\nabla_i \cdot \mathbf{R}) \mathbf{P}_R + \sum_j (\nabla_i \cdot \mathbf{R}'_j) \mathbf{P}'_j. $$
Now, from the above definitions
\begin{align*} \nabla_i \cdot \mathbf{R}_\mathrm{O} &= \frac{m}{M}\\ \nabla_i \cdot \mathbf{R} &= 0\\ \nabla_i \cdot \mathbf{R}'_j &= \delta_{ij} - \frac{m}{M}. \end{align*}
Therefore,
$$ \mathbf{P}_i = \frac{m}{M} \mathbf{P}_\mathrm{O} + \mathbf{P}'_i - \sum_j \frac{m}{M} \mathbf{P}'_j. $$
and
\begin{align*} \frac{1}{2m}\sum_i P_i^2 &= \frac{1}{2m} \left[ \frac{m^2}{M^2}\sum_i P_\mathrm{O}^2 + \sum_i P_i'^2 + \frac{m^2}{M^2}\sum_i \left( \sum_j \mathbf{P}'_j \right)^2 \right.\\ & \quad \left. + \frac{2m}{M}\mathbf{P}_\mathrm{O} \cdot \sum_i \mathbf{P}'_i - \frac{2m^2}{M^2}\sum_i \mathbf{P}_\mathrm{O} \cdot \sum_j \mathbf{P}_j' - \frac{2m}{M}\sum_i \mathbf{P}_i' \cdot \sum_j \mathbf{P}_j' \right]\\ &= \frac{nm}{2M^2}P_\mathrm{O}^2 + \frac{1}{2m}\sum_iP_i'^2 + \frac{nm}{2M^2}\left( \sum_j \mathbf{P}'_j \right)^2 \\ & \quad + \frac{1}{M}\mathbf{P}_\mathrm{O} \cdot \sum_i \mathbf{P}'_i - \frac{nm}{M^2}\mathbf{P}_\mathrm{O} \cdot \sum_i \mathbf{P}'_i - \frac{1}{M} \left( \sum_i \mathbf{P}_i' \right)^2 \end{align*}
Similarly, for the nuclear positions:
$$ \mathbf{P}_\alpha = (\nabla_\alpha \cdot \mathbf{R}_\mathrm{O}) \mathbf{P}_\mathrm{O} + (\nabla_\alpha \cdot \mathbf{R}) \mathbf{P}_R + \sum_j (\nabla_\alpha \cdot \mathbf{R}_j) \mathbf{P}'_j, $$
where
\begin{align*} \nabla_\alpha \cdot \mathbf{R}_\mathrm{O} &= \frac{M_\alpha}{M}\\ \nabla_\alpha \cdot \mathbf{R} &= (-1)^\alpha\\ \nabla_\alpha \cdot \mathbf{R}'_j &= - \frac{M_\alpha}{M}. \end{align*}
Therefore,
\begin{align*} \frac{1}{2M_1}P_1^2 &= \frac{1}{2M_1} \left[ \frac{M_1}{M}P_\mathrm{O}^2 + P_R^2 + \frac{M_1^2}{M^2} \left(\sum_j \mathbf{P}'_j\right)^2 \right.\\ & \quad \left. - \frac{2M_1}{M} \mathbf{P}_\mathrm{O} \cdot \mathbf{P}_R -2 \frac{M_1^2}{M^2}\mathbf{P}_\mathrm{O} \cdot \sum_j \mathbf{P}'_j + 2 \frac{M_1}{M}\mathbf{P}_R \cdot \sum_j \mathbf{P}'_j \right]\\ &= \frac{M_1}{2M^2}P_\mathrm{O}^2 + \frac{1}{2M_1}P_R^2 + \frac{M_1}{2M^2}\left(\sum_j \mathbf{P}'_j\right)^2\\ & \quad -\frac{1}{M}\mathbf{P}_\mathrm{O} \cdot \mathbf{P}_R - \frac{M_1}{M^2}\mathbf{P}_\mathrm{O} \cdot \sum_j \mathbf{P}'_j + \frac{1}{M}\mathbf{P}_R \cdot \sum_j \mathbf{P}'_j. \end{align*}
Similarly,
\begin{align*} \frac{1}{2M_2}P_2^2 &= \frac{M_2}{2M^2}P_\mathrm{O}^2 + \frac{1}{2M_2}P_R^2 + \frac{M_2}{2M^2}\left(\sum_j \mathbf{P}'_j\right)^2\\ & \quad +\frac{1}{M}\mathbf{P}_\mathrm{O} \cdot \mathbf{P}_R - \frac{M_2}{M^2}\mathbf{P}_\mathrm{O} \cdot \sum_j \mathbf{P}'_j - \frac{1}{M}\mathbf{P}_R \cdot \sum_j \mathbf{P}'_j. \end{align*}
Summing these formulas gives the transformed form of the kinetic energy operator: $$ T = \frac{1}{2M}P^2_\mathrm{O} + \frac{1}{2\mu}P^2_\mathrm{R} + \frac{1}{2m}\sum_{i=1}^n {P}_i'^2 - \frac{1}{2M} \sum_{i,j=1}^n \mathbf{P}_i' \cdot \mathbf{P}_j', $$ where \(\mu = M_1M_2 / (M_1 + M_2)\) is known as the reduced mass of the nuclei.
Collecting together like terms in the sum gives: \begin{align*} T &= \left( \frac{nm}{2M^2} + \frac{M_1}{2M^2} + \frac{M_2}{2M^2} \right)P^2_\mathrm{O} + \left( \frac{1}{2M_1} + \frac{1}{2M_2} \right)P^2_\mathrm{R}\\\\ & + \frac{1}{2m}\sum_{i=1}^n {P}_i'^2 + \left(\frac{nm}{2M^2} + \frac{M_1}{2M^2} - \frac{M_2}{2M^2} - \frac{1}{M}\right) \sum_{i,j=1}^n \mathbf{P}_i' \cdot \mathbf{P}_j'\\\\ & + \left(\frac{1}{M} - \frac{1}{M}\right)\mathbf{P}_\mathrm{O} \cdot \mathbf{P}_R + \left(\frac{1}{M} - \frac{1}{M}\right)\mathbf{P}_\mathrm{R} \cdot \sum_j \mathbf{P}'_j\\ & + \left( \frac{1}{M} - \frac{M_1}{M^2} - \frac{M_2}{M^2} - \frac{nm}{M^2} \right) \mathbf{P}_\mathrm{O} \cdot \sum_i \mathbf{P}'_i, \end{align*} where we have used the identity $$ \left(\sum_j \mathbf{P}'_j\right)^2 = \sum_{i,j=1}^n \mathbf{P}_i' \cdot \mathbf{P}_j'. $$ Further simplification is achieved using the relation $$ \frac{1}{\mu} = \frac{1}{M_1} + \frac{1}{M_2} $$ and the definition $M=M_1 + M_2 + nm$ to give the above equation for $T$.
The four terms in this equation are, respectively: the translational kinetic energy of the molecule as a whole, the relative kinetic energy of the nuclei (rotational and vibrational), the kinetic energy of the electrons relative to the centre of mass, and a term known as the mass polarization term which accounts for small fluctuations in the position of the centre of mass as the electrons move around.
In the absence of externally-applied fields space is isotropic and so in this case the wavefunction can be rigorously factorized into a part describing the translational motion of the molecule as a whole and a part describing everything else. Correspondingly, we will drop the first term in the kinetic energy operator to focus on the internal motions of the molecule.