Transforming the molecular kinetic energy operator to an origin at the centre of mass of the nuclei

This previous article derived the form of the kinetic energy operator for a diatomic molecule with the space-fixed origin at the molecular centre of mass:

$$ T = \frac{1}{2M}P^2_\mathrm{O} + \frac{1}{2\mu}P^2_R + \frac{1}{2m}\sum_{i=1}^n {P}_i'^2 - \frac{1}{2M} \sum_{i,j=1}^n \boldsymbol{P}_i' \cdot \boldsymbol{P}_j', $$

where $\mu = M_1M_2 / (M_1 + M_2)$ is the reduced mass of the nuclei, $m$ is the electron mass, $M = M_1 + M_2 + nm$ is the total molecular mass (including the $n$ electrons), and $\boldsymbol{P}_\mathrm{O}$, $\boldsymbol{P}_R$ and $\boldsymbol{P}_i'$ are the momenta conjugate to the coordinates of the molecular centre of mass, internuclear distance and electrons respectively.

We now want to transform the coordinate system further so that its origin lies at the centre of mass of the nuclei, located at:

$$ \boldsymbol{R}_\mathrm{N}' = \frac{1}{M_1+M_2} \sum_{\alpha=1}^2 M_\alpha \boldsymbol{R}_\alpha'. $$

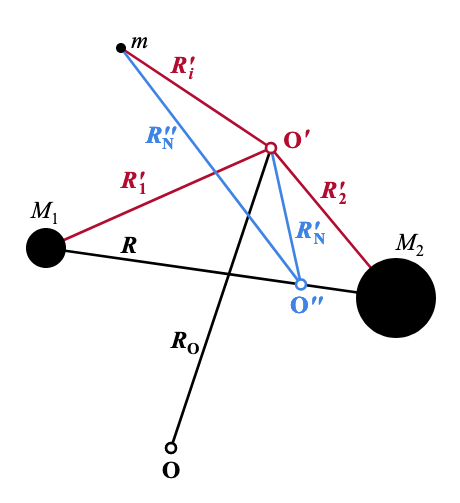
The coordinate system transformation from an origin at the molecular cente of mass (O', primed vectors) to one with its origin at the centre of mass of the nuclei (O'', double-primed vectors).

In this new coordinate system, the electrons have position vectors $\boldsymbol{R}_i'' = \boldsymbol{R}_i' - \boldsymbol{R}_\mathrm{N}'$. But from the definition of the molecular centre of the mass,

$$ m\sum_i \mathbf{R}_i' + \sum_\alpha M_\alpha \mathbf{R}_\alpha' = 0 $$

it follows that

$$ \boldsymbol{R}_i'' = \boldsymbol{R}_i' +\frac{m}{M_1 + M_2} \sum_{i=1}^n \boldsymbol{R}_i'. $$

Our goal is to transform the kinetic energy operator above into a form involving the electron momenta in this new coordinate system, $\boldsymbol{P}_j''$. From the chain rule,

$$ \boldsymbol{P}_i' = \sum_{j=1}^n (\nabla_i' \cdot \boldsymbol{R}_j'') \boldsymbol{P}_j'', $$

where

$$ \nabla_i' \cdot \boldsymbol{R}_j'' = \delta_{ij} + \frac{m}{M_1 + M_2}. $$

Therefore,

\begin{align*} - \frac{1}{2M} \sum_{i,j=1}^n \boldsymbol{P}_i' \cdot \boldsymbol{P}_j' &= -\frac{1}{2M} \sum_{i,j} \left[ \boldsymbol{P}_i'' \cdot \boldsymbol{P}_j'' + \frac{2m}{M_1 + M_2}\sum_{k} \boldsymbol{P}_i'' \cdot \boldsymbol{P}_k'' + \frac{m^2}{(M_1 + M_2)^2}\sum_{k,l} \boldsymbol{P}_k'' \cdot \boldsymbol{P}_l'' \right]\\ &= -\frac{1}{2M} \left[ 1 + \frac{2nm}{M_1 + M_2} + \frac{n^2m^2}{(M_1 + M_2)^2} \right] \sum_{i,j} \boldsymbol{P}_i'' \cdot \boldsymbol{P}_j'' \end{align*}

and

\begin{align*} \frac{1}{2m} \sum_{i=1}^n {P}_i'^2 &= \frac{1}{2m} \left[ \sum_i {P}_i{''}^2 + \frac{2m}{M_1 + M_2} \sum_{i,j}\boldsymbol{P}_i'' \cdot \boldsymbol{P}_j'' + \frac{m^2}{(M_1 + M_2)^2}\sum_{i,j,k} \boldsymbol{P}_j'' \cdot \boldsymbol{P}_k'' \right]\\ &= \frac{1}{2m} \sum_i {P}_i{''}^2 + \frac{1}{M_1 + M_2} \sum_{i,j}\boldsymbol{P}_i'' \cdot \boldsymbol{P}_j'' + \frac{nm}{2(M_1 + M_2)^2}\sum_{i,j} \boldsymbol{P}_i'' \cdot \boldsymbol{P}_j''. \end{align*}

Substituting these two equations into that for $T$ above gives: $$ T = \frac{1}{2M}P^2_\mathrm{O} + \frac{1}{2\mu}P^2_R + \frac{1}{2m}\sum_{i=1}^n {P}_i^{''2} - \frac{1}{2(M_1 + M_2)} \sum_{i,j=1}^n \boldsymbol{P}_i'' \cdot \boldsymbol{P}_j''. $$