Solution P6.6.3
The code below tracks the bacteria positions over time on a two-dimensional plot (see Section 7.5.2 for a description of Matplotlib's imshow function.)
import numpy as np
import matplotlib.pyplot as plt
# The bacteria "world"
n = 100
world = np.zeros((n+1,n+1))
# Magnitude of step size
d = 0.02
# Number of bacteria, number of steps for each bacterium
nb, nsteps = 10, 400
# Position of the attractant
cx = cy = 0.5
# P0 is the probability of tumbling when heading toward the attractant; P1 is
# the probability of tumbling when heading away from it.
P0, P1 = 0.7, 1
def tumble():
"""Randomly pick a new direction, (dx, dy) for the bacterium."""
theta = np.random.rand() * np.pi * 2
return d * np.cos(theta), d * np.sin(theta)
def fpot(x, y):
"""Food potential, decreasing linearly as from (cx, cy)."""
return -np.hypot((x-cx), (y-cy))
for b in range(nb):
# Start the bacteria off evenly-spaced around the unit circle centred on
# (cx, cy).
phi = 2*np.pi*b/nb
x, y = cx + np.cos(phi)/2, cy + np.sin(phi)/2
# Randomly pick an initial direction for the bacterium
dx, dy = tumble()
for i in range(nsteps):
# We will estimate the gradient as proportional to the difference
# between the food potential at the next position, (x',y') and that at
# the # current position: grad ∝ fpot(x',y') - fpot(x,y)
grad = -fpot(x,y)
# Update the bactrium's position (wrapping round at the world's edges
x, y = max(min(x+dx, 1), 0), max(min(y+dy, 1), 0)
ix, iy = int(x * n), int(y * n)
world[ix, iy] = 1
# So the attractant gradient at the new position is:
grad += fpot(x,y)
if grad < 0:
# We're moving away from the attractant: definitely tumble
prob = P1
else:
# We're not moving away, tumble only with this probability
prob = P0
# Decide whethe to tumble and update direction of movement if we do
if np.random.rand() < prob:
dx, dy = tumble()
plt.imshow(world, cmap='hot')
plt.show()
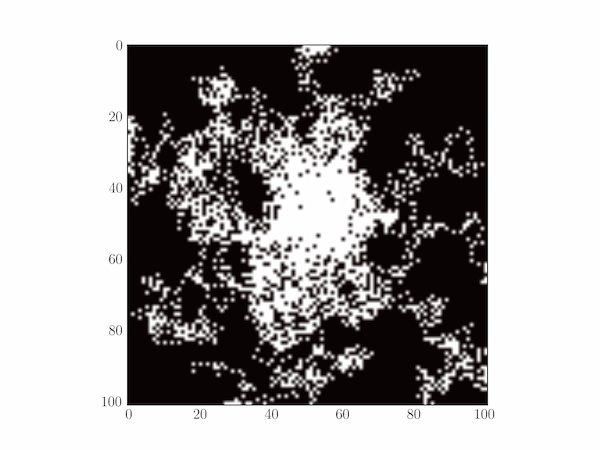
A typical plot is depicted below.