Question
The Women's Olympic Heptathlon is comprised of seven events in which competitors are awarded points based on their performance. The points are awarded according to the following formulas for the different groups of events (running, jumping, throwing). The formulas are devised to award 1000 points for some reference performance and 0 points at some minimum level of performance.
-
Running: $P = a(b-T)^c$ (time, $T$ in seconds)
-
Jumping: $P = a(H-b)^c$ (height, $H$ in cm)
-
Throwing: $P = a(D-b)^c$ (distance, $D$ in m)
The coefficients for these formulas are given for each event in the table below.
| Event | $a$ | $b$ | $c$ |
|---|---|---|---|
| 100 m hurdles | 9.23076 | 26.7 | 1.835 |
| High jump | 1.84523 | 75 | 1.348 |
| Shot put | 56.0211 | 1.50 | 1.05 |
| 200 m | 4.99087 | 42.5 | 1.81 |
| Long jump | 0.188807 | 210 | 1.41 |
| Javelin throw | 15.9803 | 3.80 | 1.04 |
| 800 m | 0.11193 | 254 | 1.88 |
At the 2016 Rio Olympics the competitors awarded medals performed as given in this table.
| Event | Nafissatou Thiam | Jessica Ennis-Hill | Brianne Theisen Eaton |
|---|---|---|---|
| 100 m hurdles | 13.56 s | 12.84 s | 13.18 s |
| High jump | 1.98 m | 1.89 m | 1.86 m |
| Shot put | 14.91 m | 13.86 m | 13.45 m |
| 200 m | 25.10 s | 23.49 s | 24.18 s |
| Long jump | 6.58 m | 6.34 m | 6.48 m |
| Javelin throw | 53.13 m | 46.06 m | 47.36 m |
| 800 m | 2 min 16.54 sec | 2 min 9.07 sec | 2 min 9.50 sec |
Write a Python program to store the coefficients in a dictionary, keyed by the event name, and use another dictionary to store the competitors' results in each event. Use these data structures. Define functions to calculate the points a given performance is awarded in each event, and use them to calculate the total number of points for each of the competitors.
Bonus exercise: Generate the following diagram as an SVG image.
Hints: the following function returns a point on the unit circle a fraction i/n of the way round from a reference direction defined by phase (use phase=0 to use the $x$-axis as this refefence direction).
def get_point_on_unit_circle(i, n, phase=0):
return np.cos(2*np.pi*i/n - phase), np.sin(2*np.pi*i/n - phase)
Find the distances along each event axis in pixel coordinates with:
r_pts = r * (event_points - min_points) / (max_points - min_points)
where min_points and max_points correspond to the centre and outer limit of the chart axes respectively (500 and 1300 are good choices here) and r is the radius of the chart in pixels.
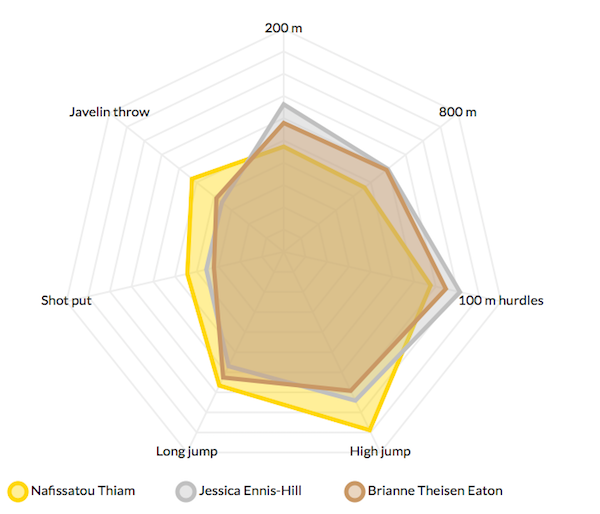
This figure was inspired by @kala_blanc's visualization on Twitter.
Solution
Here is one approach. The output is:
Nafissatou Thiam: 6810
Jessica Ennis-Hill: 6775
Brianne Theisen Eaton: 6653
which can be verified e.g. here.
import numpy as np
# Some colour definitions.
LIGHT_GREY = '#eeeeee'
GOLD = '#ffd700'
SILVER = '#c0c0c0'
BRONZE = '#ca9865'
# An ordered list of colours for the results polygons.
colours = [GOLD, SILVER, BRONZE]
# An ordered list of women's heptathlon events.
events = ('200 m', '800 m', '100 m hurdles', 'high jump',
'long jump', 'shot put', 'javelin throw')
# Coefficients in the points calculation formulae for each event.
coeffs = {'200 m': (4.99087, 42.5, 1.81),
'800 m': (0.11193, 254, 1.88),
'100 m hurdles': (9.23076, 26.7, 1.835),
'high jump': (1.84523, 75, 1.348),
'long jump': (0.188807, 210, 1.41),
'shot put': (56.0211, 1.50, 1.05),
'javelin throw': (15.9803, 3.80, 1.04)
}
# There are three functions to use, but two of them are really the same.
running_func = lambda T, coeffs: coeffs[0] * (coeffs[1] - T)**coeffs[2]
jumping_func = lambda H, coeffs: coeffs[0] * (H - coeffs[1])**coeffs[2]
throwing_func = jumping_func
# Create a dictionary of points-calculation functions, keyed by event name.
points_func = {'200 m': running_func, '800 m': running_func,
'100 m hurdles': running_func, 'high jump': jumping_func,
'long jump': jumping_func, 'shot put': throwing_func,
'javelin throw': throwing_func
}
# Here are the Rio 2016 performances for each of the top three competitors.
results = {
'Nafissatou Thiam': {'100 m hurdles': 13.56,
'high jump': 198,
'shot put': 14.91,
'200 m': 25.10,
'long jump': 658,
'javelin throw': 53.13,
'800 m': 136.54
},
'Jessica Ennis-Hill': {'100 m hurdles': 12.84,
'high jump': 189,
'shot put': 13.86,
'200 m': 23.49,
'long jump': 634,
'javelin throw': 46.06,
'800 m': 129.07
},
'Brianne Theisen Eaton': {'100 m hurdles': 13.18,
'high jump': 186,
'shot put': 13.45,
'200 m': 24.18,
'long jump': 648,
'javelin throw': 47.36,
'800 m': 129.50
},
}
# An ordered list of the competitors' names.
competitors = ['Nafissatou Thiam','Jessica Ennis-Hill','Brianne Theisen Eaton']
# Calculate a dictionary of points each competitor was awarded in each event.
points = {}
for competitor in competitors:
points[competitor] = {}
for event, result in results[competitor].items():
points[competitor][event] = int(
points_func[event](result, coeffs[event]))
# Report the total number of points for this competitor.
print('{}: {}'.format(competitor, sum(points[competitor].values())))
def get_point_on_unit_circle(i, n, phase=0):
"""Return the coordinates of a point i/n of the way round the unit circle.
Set phase to an angle in radians to change the "starting point" or
reference direction to use. phase=0 corresponds to the x-axis.
"""
return np.cos(2*np.pi*i/n - phase), np.sin(2*np.pi*i/n - phase)
def make_web(n, m):
"""Make the web-like axes.
Returns the SVG code for the coordinate axes forming the chart background.
This "web" has n "spokes" and m joining lines between each spoke.
"""
svg = []
svg.append('<g style="stroke-width: 2; stroke: {};">'.format(LIGHT_GREY))
for i in range(n):
# Spokes
xx, yy = get_point_on_unit_circle(i, n, phase)
x = cx + r * xx
y = cy + r * yy
svg.append('<line x1="{}" y1="{}" x2="{}" y2="{}"/>'.format(cx,cy,x,y))
# Add the joining lines between this spoke and the next one.
for j in range(1,m+1):
rr = r * j/m
x1 = cx + rr * xx
y1 = cy + rr * yy
xxp, yyp = get_point_on_unit_circle(i+1, n, phase)
x2 = cx + rr * xxp
y2 = cy + rr * yyp
svg.append('<line x1="{}" y1="{}" x2="{}" y2="{}"/>'
.format(x1,y1,x2,y2))
svg.append('</g>')
return '\n'.join(svg)
def make_event_labels():
"""Add text event labels to the vertices of the axes web."""
svg = ['<g style="font-family: Lato; font-size: 16;">']
for i,event in enumerate(events):
xx, yy = get_point_on_unit_circle(i, n, phase)
x = cx + r * xx
y = cy + r * yy
svg.append('<text x="{}" y="{}" text-anchor="middle"'
' dominant-baseline="middle">{}</text>'
.format(x, y, event.capitalize()))
svg.append('</g>')
return '\n'.join(svg)
def make_competitor_poly(competitor, colour):
"""Draw the polygon for competitor in a given colour."""
vertices = []
for i,event in enumerate(events):
event_points = points[competitor][event]
# Scale the points onto a number of pixes on the figure.
r_pts = r * (event_points - min_points) / (max_points - min_points)
xx, yy = get_point_on_unit_circle(i, n, phase)
vertices.append((cx + r_pts * xx, cy + r_pts * yy))
# Convert the list of (x,y) tuples to a string: 'x1,y1 x2,y2 ...'.
s_vertices = ' '.join(['{}, {}'.format(x,y) for (x,y) in vertices])
svg_poly = ('<polygon points="{points}" style="fill: {colour};'
' fill-opacity: 0.4; stroke-width: 5; stroke: {colour};"/>'
.format(points=s_vertices, colour=colour))
return svg_poly
def make_competitor_label(competitor, i):
"""Add a label and medal symbol for competitor indexed at i."""
tx = padding + i * (width-padding*2)//3
ty = height - padding//2
competitor_label = ('<text x="{}" y="{}" style="font-family: Lato;'
' font-size: 16; dominant-baseline: middle;">{}</text>'
.format(tx, ty, competitor))
medal_symbol = ('<circle cx="{cx}" cy="{cy}" r="10" style="fill: {colour};'
' fill-opacity: 0.4; stroke-width: 5; stroke: {colour};"/>'
.format(cx=tx-15, cy=ty, colour=colours[i]))
return '\n'.join([competitor_label, medal_symbol])
def make_svg():
"""Make and return the SVG for the heptathlon results figure."""
svg = ['<?xml version="1.0" encoding="utf-8"?>',
'<svg width="{}" height="{}" version="1.1"'
' xmlns="http://www.w3.org/2000/svg">'.format(width, height)]
svg.append('<defs><style type="text/css">'
'@import url("http://fonts.googleapis.com/css?family=Lato");'
'</style></defs>')
svg.append(make_web(n, 10))
for i, competitor in enumerate(competitors):
svg.append(make_competitor_poly(competitor, colours[i]))
svg.append(make_competitor_label(competitor, i))
svg.append(make_event_labels())
svg.append('</svg>')
return svg
# Figure dimensions and padding of content from each of the figure edges.
width, height, padding = 600, 600, 40
# The centre of the figure
cx, cy = width//2, height//2
# The axes therefore have pixel dimensions given by r.
r = min(width, height)//2 - padding
# We want the first axis pointing along the y-axis of the figure.
phase = np.pi / 2
# Scale the figure so that the axes range from min_points to max_points.
min_points, max_points = 500, 1300
# The total number of events (7 for a heptathlon)
n = len(events)
# Finally, write the SVG file.
with open('heptathlon.svg', 'w') as fo:
print('\n'.join(make_svg()), file=fo)