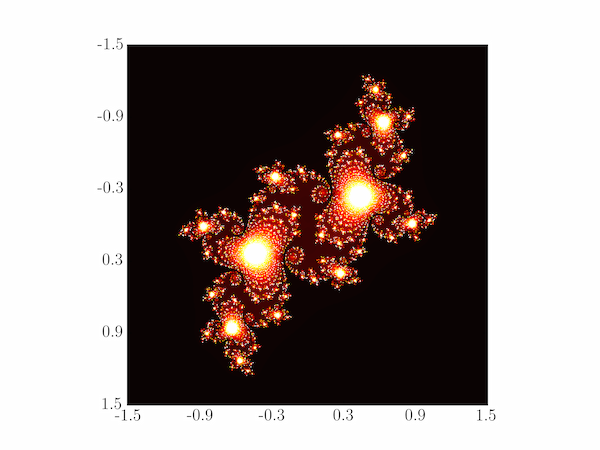
Solution P7.2.4
The code below is one way of plotting the required Julia set. There are many different ways of picking the pixel colours.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
# Image width and height; parameters for the plot
im_width, im_height = 500, 500
c = complex(-0.1, 0.65)
zabs_max = 10
nit_max = 1000
xmin, xmax = -1.5, 1.5
xwidth = xmax - xmin
ymin, ymax = -1.5, 1.5
yheight = ymax - ymin
julia = np.zeros((im_width, im_height))
for ix in range(im_width):
for iy in range(im_height):
nit = 0
# Map pixel position to a point in the complex plane
z = complex(ix / im_width * xwidth + xmin,
iy / im_height * yheight + ymin)
# Do the iterations
while abs(z) <= zabs_max and nit < nit_max:
z = z**2 + c
nit += 1
shade = 1-np.sqrt(nit / nit_max)
ratio = nit / nit_max
julia[ix,iy] = ratio
fig, ax = plt.subplots()
ax.imshow(julia, interpolation='nearest', cmap=cm.hot)
# Set the tick labels to the coordinates of z0 in the complex plane
xtick_labels = np.linspace(xmin, xmax, xwidth / 0.5)
ax.set_xticks([(x-xmin) / xwidth * im_width for x in xtick_labels])
ax.set_xticklabels(['{:.1f}'.format(xtick) for xtick in xtick_labels])
ytick_labels = np.linspace(ymin, ymax, yheight / 0.5)
ax.set_yticks([(y-ymin) / yheight * im_height for y in ytick_labels])
ax.set_yticklabels(['{:.1f}'.format(ytick) for ytick in ytick_labels])
plt.show()