Animating a decaying sine curve 1

Learning Scientific Programming with Python (2nd edition)

E7.28: Animating a decaying sine curve 1

The following code animates a decaying sine curve that could, for example, represent the decaying chime of a struck tuning fork at a fixed frequency: $$ M(t) = \sin(2\pi f t)\mathrm{e}^{-\alpha t} $$

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# Time step for the animation (s), max time to animate for (s).
dt, tmax = 0.01, 5
# Signal frequency (s-1), decay constant (s-1).
f, alpha = 2.5, 1
# These lists will hold the data to plot.
t, M = [], []

# Draw an empty plot, but preset the plot x- and y-limits.
fig, ax = plt.subplots()
(line,) = ax.plot([], [])
ax.set_xlim(0, tmax)
ax.set_ylim(-1, 1)
ax.set_xlabel("t /s")
ax.set_ylabel("M (arb. units)")


def animate(i):
    """Draw the frame i of the animation."""

    global t, M
    # Append this time point and its data and set the plotted line data.
    _t = i * dt
    t.append(_t)
    M.append(np.sin(2 * np.pi * f * _t) * np.exp(-alpha * _t))
    line.set_data(t, M)


# Interval between frames in ms, total number of frames to use.
interval, nframes = 1000 * dt, int(tmax / dt)
# Animate once (set repeat=False so the animation doesn't loop).
ani = animation.FuncAnimation(
    fig, animate, frames=nframes, repeat=False, interval=interval
)
plt.show()

Recall that the ax.plot method returns a tuple of Line2D objects, even if there is only one plotted line. We need to retain a reference to it so we can set its data in the animation function, animate.
By declaring the t and M lists to be global objects we can modify them from inside the animate function.
By setting the time interval between frames to be the same (in milliseconds) as the time step, the animation is made to appear "in real time."

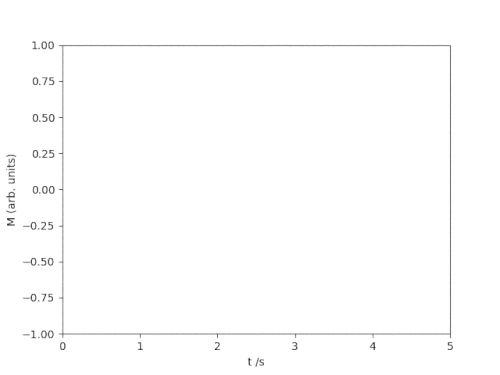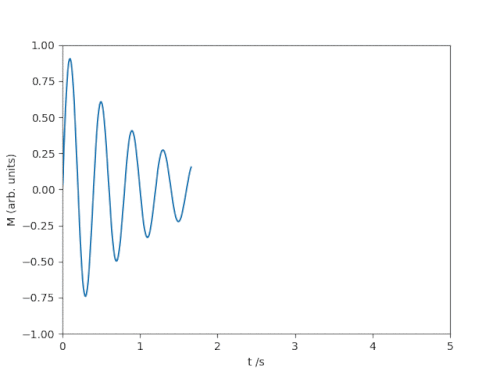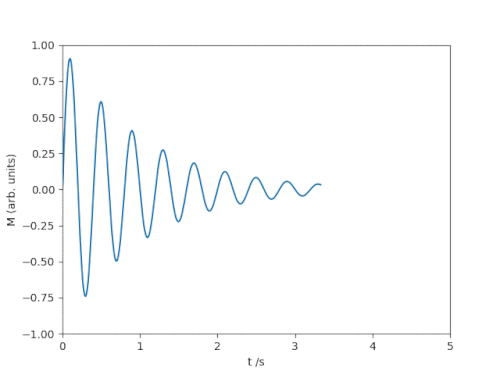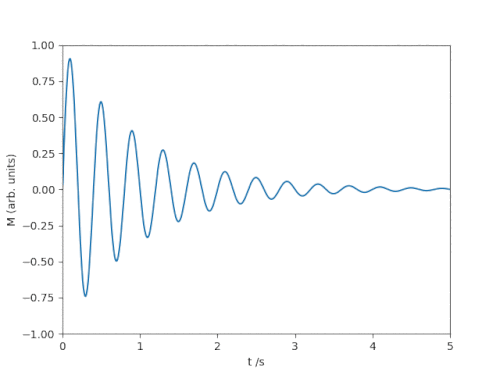
Matplotlib animation of a ringdown process.