Learning Scientific Programming with Python (2nd edition)
P6.1.2: The shoelace algorithm
Question P6.1.2
The shoelace algorithm for calculating the area of a simple polygon (that is, one without holes or self-intersections) proceeds as follows: Write down the $(x,y)$ coordinates of the $N$ vertices in an $N \times 2$ array and then repeat the coordinates of the first vertex as the last row to make an $(N+1) \times 2$ array. Now (a) multiply each $x$-coordinate value in the first $N$ rows by the $y$-coordinate value in the next row down and take the sum, $S_1 = x_1y_2 + x_2y_3 + \cdots + x_Ny_1$. Then (b) multiply each $y$-coordinate value in the first $N$ rows by the $x$ coordinate in the next row down and take the sum, $S_2 = y_1x_2 + y_2x_3 + \cdots + y_Nx_1$. The area of the polygon is then $\frac{1}{2}|S_1-S_2|$.

Implement this algorithm as a function that takes a NumPy array of vertices as its argument and returns the area of the polygon. Do not use Python loops!
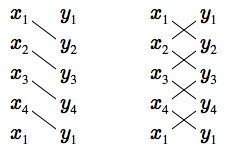
A depiction of the shoelace algorithm for calculating the area of a simple polygon.